asd Dickens: calka podwojna ∬(x²+4y+9)dxdy bo obszarze D: x² + y² ≤ 4 liczyłem dwa razy i wychodzi mi 40π, w książce mam odpowiedź 56π, może ktoś sprawdzić jaki jest poprawny wynik?

jc: 4+36=40.

jc: Dobrze masz, w odpowiedzi jest błąd.

Dickens: dzieki

Dickens: Czy jest jakis kalkulator do całek podwójnych bo znowu wychodzi mi inny wynik niz w odpowiedziach, liczone dwa razy ∬xdxdy po obszarze D: y= −x² y=√x y = x−2

	24		141
wychodzi mi		a w odpowiedzi jest
	5		20

Adamm: możesz wpisać całkę w wolfram alpha poczytaj o tym http://reference.wolfram.com/language/ref/Integrate.html

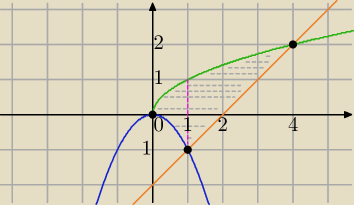
Mila: −x²=x−2 x²+x−2=0 x=1 lub x=−2 √x=x−2 i x>2 x=4 ₀∫1[ _−x²∫^√x(x) dy ]dx+₁∫⁴[ _y=(x−2)∫^√x(x) dy ]dx=J₁+J₂

	2		1		13
J1=0∫1([x*y]−x2√x )=0∫1(x3/2+x3) dx=[		x5/2+		x4]01=
	5		4		20

	2		1
j2=1∫4(x3{2}−x2+2x) dx=[		x5/2−		x3+x2}]14=
	5		3

	2		1		2		1		32
=		*√45−		*64+16−		+		−1=
	5		3		5		3		5

13		32		141
	+		=
20		5		20

Dickens: Dziekuje bardzo