Krzywa Beziera Ada: Podać warunki dla których dwa segmenty krzywej Beziera mają ciągłość C¹ w punkcie połączenia. Podać przykład połączenia gdzie pierwszy segment krzywej Beziera jest określony następującymi punktami kontrolnymi P₀ = [0,0] P₁ = [1,5] P₂ = [4,5] P₃ = [5,0]. Pomoże ktoś?

Ada: Proszę o pomoc

a7: nie ma "Pytającego", w tym linku jest fragment o łączeniu krzywych, gdzie sa zdefiniowane warunki może to coś pomoże ( fragment "Łączenie krzywych Béziera" ) http://smurf.mimuw.edu.pl/external_slides/Modelowanie_obiektowe/Modelowanie_obiektowe.html

a7: strona 52 są te warunki ciągłości http://lucc.pl/inf/grafika_komputerowa/jarnicki_wyklady/wyklady.pdf

Pytający: Jestem, jestem, acz nie zawsze tu. To jeszcze przykład połączenia: P₃−P₂=[5,0]−[4,5]=[1,−5] // wektor kierunkowy Więc punkty kontrolne drugiego segmentu: R₀=P₃ R₁=P₃+α*[1,−5], α>0 // α możesz wybrać jakie chcesz, np. R₁=[6,−5] dla α=1 R₂, R₃ dowolne (różne od poprzednich)

Ada: Bardzo dziękuje R₂ i R₃ różnią się od R₁ wartością α?

Pytający: Nie, R₂ i R₃ są zupełnie dowolne. W zasadzie to mogą być takie same jak R₁, ale wtedy będzie "mniej ciekawie wyglądało".

Ola: Hej, mam podobne zadanie jak koleżanka wyżej do rozwiązania na kolokwium ale muszę narysować przykłąd połączenia, a nie tylko go podać. Rysunek w zadaniu wygląda następująco: https://zapodaj.net/6910ade7dbfed.png.html . Czyli jeżeli R₀=[5,0], R₁=[1,−5] to mogę sobie przyjąć że np. R₂=[1,−5] i R₃=[0,0] i po zaznaczeniu tych punktów na rysunku zadanie będzie prawidłowo rozwiązane? Pozdrawiam i strasznie bardzo proszę o odpowiedź, to kolokwium jest dla mnie bardzo ważne

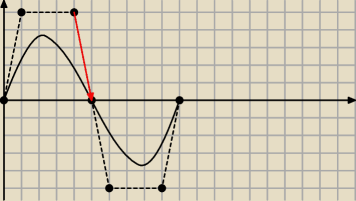
Pytający: Hej, tak strasznie prosisz, że aż z tego strachu odpowiem. R₁ musi leżeć na "przedłużeniu" wektora P₂P₃ (lub P₂R₀, to jest to samo, bo P₃=R₀), więc R₁=[1,−5] nie jest prawidłowe, jak wcześniej napisałem: "R₁=P₃+α*[1,−5], α>0 // α możesz wybrać jakie chcesz, np. R₁=[6,−5] dla α=1" Jak dla mnie najprościej byłoby przedłużyć jako swego rodzaju "sinusoidę". Wystarczy ten fragment z przedziału <0,5> przesunąć o 5 w prawo na przedział <5,10> i odbić względem OX. Wyjdzie mniej więcej jak na rysunku. P₀=[0,0], P₁=[1,5], P₂=[4,5], P₃=[5,0] R₀=[5,0], R₁=[6,−5], R₂=[9,−5], R₃=[10,0] Najważniejsze, żeby punkty: • P₂, • P₃=R₀, • R₁ leżały na jednej prostej (i w takiej kolejności).