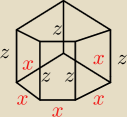
ekstrema Dawid: Zadanie na ekstrema Witam mam obliczyć maksymalną objętość zbiornika w kształcie graniastosłupa prawidłowego pięciokątnego o boku z wiedząc, że jego powierzchnia całkowita wynosi S[m2] P_c=S S=2P_p+P_b V=P_p*z Więc :

	−Pb+S
Pp=
	2

Czy dobrym myślę? Jeśli nie poproszę o jakaś podpowiedź . Dziękuje

Jerzy: Masz liczyć V, a nie Pb

Jerzy: Musisz wyrazić objętość za pomocą jednej zmiennej.

Dawid: No tak ale by obliczyć V potrzebuję P_p bo wiem, że wysokość to "z"

a7: tu mamy wzór na pole pięciokata foremnego https://matematykaszkolna.pl/strona/984.html S=5/4x²ctg36st+5xz V=5/4x²ctg36st*z

a7: z pierwszego wyliczamy z i podstawiamy do nieco skomplikowanego wzoru sa inne pomysły?

a7: z=[S−5/4x2ctg36st]/5

a7: V=5/4x2ctg36st* [S−5/4x2ctg36st]/5

Dawid: No tylko nieco skomplikowanie się robi. Może jest prostsza metoda ?

Jerzy: z jest dane,zmienną jest X.

a7: no tak wyliczamy więc x prościej nie umiem może zaraz sie uprości to wyrażenie

Dawid: I teraz liczymy pochodną V'(x) ?

a7: nie wiem czy to nie jest zadanie z serii , że trzeba wpaść na pomysł bo obliczenia są własnie "nieco skomplikowane" jak powiedział @Dawid

a7: no tak, ale wyliczenie x nie jest takie miłe

a7: 5/4x²ctg36+5z*x −S=0 √Δ=...... mam dalej liczyć czy ktoś ma pomysł?

a7: tu jest pomyłka bo powinnysmy wziąc dwa pola posdtawy jesli iść w ogóle tym tropem 5/2x2ctg36+5zx−S=0 ?

a7: 5/2x²ctg36+5zx−S=0

a7: Δ=25z²+10ctg36*S √Δ=P{25z²+10ctg36*S} x₁=(−5z−√Δ)/(5*ctg36) x₂=(−5z+ √Δ)/(5*ctg36) następnie podstawiamy x₁ do funkcji i liczymy jej ekstremum potem to samo z x₂ po drodze może wyjść jakaś sprzeczność, to wtedy odrzucamy dane rozwiązanie ale obawiam się, że wyjdzie coś nie fajnego do liczenia może ktoś spojrzy jeszcze i coś wymysli ......

Dawid: No to się komplikuje zadanie

a7: no właśnie nawet nie bardzo sa podobne w necie,

Dawid: Ja niestety nie mam pomysłu na te zadanie może ktoś inny pomoże jeszcze

Dawid: Mam jeszcze takie zadanko Oblicz maksymalną objętość zbiornika w kształcie graniastosłupa prawidłowego trójkątnego o boku podstawy a wiedząc, że jego powierzchnia całkowita wynosi P[m2] P_c=P V=P_p*H

	a2√3
Pp=
	4

	a2√3
V=		*H
	4

Więc

	a2√3		a2√3
V'(h)=(		*H)'=
	4		4

Dobrze ?

a7: chyba tak

Mila: Czy w pierwszym bok podstawy ma długość z ? Drugie źle.

Dawid: x to długość podstawy natomiast z to wysokość

Mila: Pole 5− kąta foremnego o boku a:

	√25+10√5
P=		*a2
	4

a7: dlaczego drugie źle?

Dawid: @Mila skąd Ci taki wynik wyszedł ?

Mila: http://calcoolator.pl/obwod-pole-powierzchni-przekatna-pieciokata.html#

Dawid: Czyli S=2P_p+P_b

	x2
2Pp=		*√25+10√5
	4

	x2
Pp=		*√25+10√5
	8

	x2
V=		*√25+10√5*z ?
	8

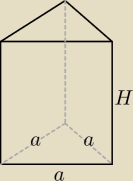
Mila: Może zacznijmy od (2). V=P_Δ*H Wiadomo, że: P_c=P

	a2√3
P=2*		+3*a*H⇔
	4

	a2√3
P−		=3*a*H
	2

	a2√3   P−   2
H=
	3a

	a2√3		a2√3   P−   2
V(a)=		*		⇔
	4		3a

	√3		1
V(a)=		*(P*a−		a3√3), a>0
	12		2

	√3		3
V'(a)=		*(P−		√3a2)
	12		2

	3√3
V'(a)=0⇔		a2=P /*√3
	2

9
	a2=√3*P
2

	2√3P		√12P
a2=		⇔a2=
	9		9

	4√12*√P
a=±
	3

	4√12*√P
dla a=		funkcja V(a) ma ekstremum
	3

	√3		2√3P		P
Vmax=		*		*H=		*H
	4		9		6

teraz podstaw do wzoru na H obliczone a ⇔

	2√P
H=
	34√12

	P*√P
Vmax=		dla a=.. i H=...
	94√12

================== Posprawdzajcie rachunki, bo może coś mi umknęło.

Dawid: Wielkie dzięki , a ktoś ma pomysł na pierwsze zadanie ?