Ekstrema Lokalne i punkty przegięcia
Ernest: Znajdź ekstrema lokalne i punkty przegięcia funkcji f(x) = x3 − 12x + 1
Zaczynamy od pochodnej Czyli
2x2 − 12 i przyrównujemy do zera :
2x2 − 12 = 0 / : 2
x2 − 6 = 0
x = √6
Co zrobić w następnym kroku ?
Bardzo proszę o pomoc
2 cze 16:21
Jerzy:
Policzyć poprawnie pochodną.
2 cze 16:26
Ernest: no dobra znalazłem błąd :
x3 − 12x + 1
3x2 − 12 = 0
3x2 = 12 / : 3
x2 = 4
x = 2
I co będzie nastepnym krokiem ?
2 cze 16:30
Jerzy: Znalezienie drugiego miejsca zerowego pochodnej.
2 cze 16:32
Ernest:
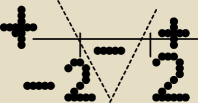
Czyli to będzie od (−
∞ do − 2 ) ( +2 +
∞) rosnąca a od (−2 do 2 ) jest malejąca
Dobrze myślę ?
2 cze 16:38
Jerzy:
Dobrze, teraz określ ekstrema lokalne i licz drugą pochodną.
2 cze 16:41
Ernest: Czyli
Ekstremum lokalne
max = −2
min = 2
druga pochodna : 6x
6x=0/6
x=0
czyli punkt przegięcia to jest 0 ?
2 cze 16:47
a7:
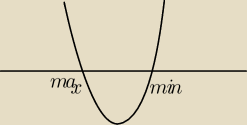
x=
√6 lub x=−
√6
robimy rysunek paraboli
mamy już maximum i minimum
potem liczymy drugą pochodną
f''(x)=4x
sprawdzamy punkt przegięcia
2 cze 16:47
a7: oj pochodna niepoprawnie policzona
2 cze 16:48
Jerzy:
Tak, punkt przegięcia to x= 0, bo druga pochodna zmienia znak.
2 cze 16:53
Ernest: Super. Dziękuję bardzo za pomoc.
2 cze 16:54
2 cze 16:55
 Czyli to będzie od (−∞ do − 2 ) ( +2 +∞) rosnąca a od (−2 do 2 ) jest malejąca
Dobrze myślę ?
Czyli to będzie od (−∞ do − 2 ) ( +2 +∞) rosnąca a od (−2 do 2 ) jest malejąca
Dobrze myślę ?
 x=√6 lub x=−√6
robimy rysunek paraboli
mamy już maximum i minimum
potem liczymy drugą pochodną
f''(x)=4x
sprawdzamy punkt przegięcia
x=√6 lub x=−√6
robimy rysunek paraboli
mamy już maximum i minimum
potem liczymy drugą pochodną
f''(x)=4x
sprawdzamy punkt przegięcia