Wykaz że Kasia: Trójkąt ABC jest prostokątny. Z punktu M należącego do przeciwprostokatnej BC poprowadzone odcinki MD I MS prostopadłe odpowiednio do przyprostokatnych AC i AB. Wykaz że ^|DM|_|AB|+^|MS|_|AC|=1

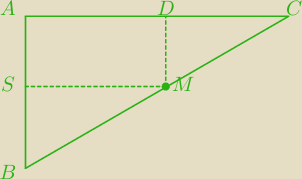
iteRacj@: AC⊥AB, DM⊥AC, SM⊥AB stąd DM∥AB, SM∥AC, ΔSBM≈ΔDMC≈ΔABC

|DM|		|CM|		|SM|		|BM|
	=		oraz		=
|AB|		|BC|		|AC|		|BC|

	|DM|
|CM|=		*|BC|
	|AB|

	|SM|
|BM|=		*|BC|
	|AC|

|CM|=|BC|−|BM|

|DM|		|SM|
	*|BC|=|BC|−		*|BC| // : |BC|
|AB|		|AC|

|DM|		|SM|
	=1−
|AB|		|AC|

|DM|		|SM|
	+		=1
|AB|		|AC|

anaisy: Z tw. Talesa

	SM		BM
SM || AC, więc		=
	AC		BC

	DM		CM
DM || AB, więc		=
	AB		CB

Stąd

DM		SM		BM + CM		BC
	+		=		=		= 1
AB		AC		BC		BC

iteRacj@: elegancko i krótko