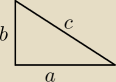
minimum matma po nocach: Obwód trójkąta prostokątnego wynosi 1. Ile wynosi maksymalne pole takiego trójkąta. a+b+c=1 ; a²+b²=c² c=1−a−b W kluczu: Oznaczenie: b− jedna z przyprostokątnych trójkąta. Znalezienie pola jako funkcji b:

	2b2−2
P=		.
	4b−4

Chodzi mi tylko o ustalenie funkcji optymalizowanej, nie mogę do niej dojść.

Lech: Policz pochodna funkcji P wzgledem zmiennej b .

Mila: a+b+c=1 a²+b²=c² −−−−−−−−−−−−− a+b=1−c /², 0<c<1 a²+2ab+b²=c²−2c+1⇔ 2ab=−2c+1⇔2ab=−2*(1−a−b)+1 2ab=−2+2a+2b+1 2ab−2a=2b−1 2a(b−1)=2b−1)

	2b−1		1
a=		i 0<a<1⇔b∊(0,		)
	2*(b−1)		2

	1		2b2−b
P(b)=		a*b=
	2		2*(2b−2)

Policzysz dalej sam?

	3		√2
Pmax=		−
	4		2

matma po nocach: Tak, dziękuję bardzo za rozpisanie

Mila: