gfd
Benio:
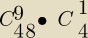
Kombinacje
Na ile sposobów z talii 52 kart można wylosować 10 kart tak,
aby był wśród nich dokładnie jeden as?
W odpowiedziach jest:
https://matematykaszkolna.pl/strona/1015.html
Dlaczego na górze C jest 9 a nie 48 ? Chyba powinno być odwrotnie − na górze C − 48 a na dole 9
bo "Kombinację k−elementowa ze zbioru n elementowego
C
nk?
Prosiłbym o wytłumaczenie tego, i dlatego nie liczymy C po prostu z tego: C
489, tylko
wymnażamy jeszcze przez jakieś C
14
1 cze 11:31
Saizou :
Tak się przyjęło zapisywać.
Jak Ci wygodniej możesz używać tylko symbolu Newtona i nie będziesz mieć zgrzytu.
1 cze 11:34
iteRacj@:
| | | |
wymnażamy przez | , bo w talii kart są cztery różne asy |
| | |
i zestaw kart z asem ♦ jest to inny zestaw niż z asem ♣
1 cze 11:43
a7: chodzi oto że z tali 52 odejmujemy 4 asy i losujemy jakby z reszty dziewięć kart i mnożemy
razy ilość sposobów w jaki z pozostałych czterch asów można wylosować jednego
1 cze 11:54
a7: w sumie wylosowaliśmy 10 kart z czego jeden as z czterech asów oraz 9 kart z pozostałych 48
kart
1 cze 11:56
a7: a zapis to kwestia, że tak jest przyjęte , może to mało intuicyjne, ale trzeba (i można) się
przyzwyczaić
1 cze 11:57
a7: | | | |
gdybyś losował dowolne 10 z 52 kart to byś miał | |
| | |
ale ty losujesz tak, żeby był tylko jeden as czyli 9 dowolnych kart (z czterdziestu osmiu, bo
nie możesz dać możliwości, aby tam się znalazł przypadkiem którykolwiek as i z asów
jednego
czyli
1 cze 12:06
Jerzy:
Albo: 4*48*47*46*45*44*43*42*41*40
1 cze 12:09
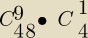 Kombinacje
Na ile sposobów z talii 52 kart można wylosować 10 kart tak,
aby był wśród nich dokładnie jeden as?
W odpowiedziach jest:
https://matematykaszkolna.pl/strona/1015.html
Dlaczego na górze C jest 9 a nie 48 ? Chyba powinno być odwrotnie − na górze C − 48 a na dole 9
bo "Kombinację k−elementowa ze zbioru n elementowego
Cnk?
Prosiłbym o wytłumaczenie tego, i dlatego nie liczymy C po prostu z tego: C489, tylko
wymnażamy jeszcze przez jakieś C14
Kombinacje
Na ile sposobów z talii 52 kart można wylosować 10 kart tak,
aby był wśród nich dokładnie jeden as?
W odpowiedziach jest:
https://matematykaszkolna.pl/strona/1015.html
Dlaczego na górze C jest 9 a nie 48 ? Chyba powinno być odwrotnie − na górze C − 48 a na dole 9
bo "Kombinację k−elementowa ze zbioru n elementowego
Cnk?
Prosiłbym o wytłumaczenie tego, i dlatego nie liczymy C po prostu z tego: C489, tylko
wymnażamy jeszcze przez jakieś C14