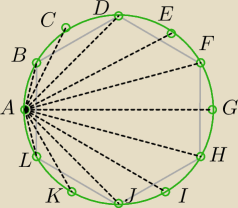
wartość oczekiwana zmiennej losowej iteRacj@: W okrąg o promieniu długości 1 wpisano dwunastokąt foremny. Ze zbioru jego wierzchołków wybieramy losowo dwa różne, przy czym każdy wybór jest jednakowo prawdobodobny. Wybrane punkty dzielą okrąg na dwa łuki. Długość największego z tych łuków jest wartością zmiennej losowej. Oblicz wartość oczekiwaną tej zmiennej losowej. Proszę o sprawdzenie mojego rozwiązania. z każdego wierzchołka można poprowadzić po jedenaście cięciw czyli 11 różnych podziałów na łuki, otrzymujemy pary łuków o długościach

1		11
	*2π+		*2π;
12		12

2		10
	*2π+		*2π;
12		12

3		9
	*2π+		*2π;
12		12

4		8
	*2π+		*2π;
12		12

5		7
	*2π+		*2π;
12		12

6		6
	*2π+		*2π;
12		12

	11		2
P(X=		*2π)=		wylosowano wierzchołki AB, AL
	12		11

	10		2
P(X=		*2π)=		wylosowano wierzchołki AC, AK
	12		11

	9		2
P(X=		*2π)=		wylosowano wierzchołki AD, AJ
	12		11

	8		2
P(X=		*2π)=		wylosowano wierzchołki AE, AI
	12		11

	7		2
P(X=		*2π)=		wylosowano wierzchołki AF, AH
	12		11

	6		1
P(X=		*2π)=		wylosowano wierzchołki AG
	12		11

	3		6π
EX=2π(1/12*2/11+2/12*2/11+3/12*2/11+4/12*2/11+5/12*2/11+6/12*1/11)=2π		=
	11		11

a7: na pierwszy rzut oka wygląda bardzo elegancko i moim zdaniem dobre, ale zaraz jeszcze się spróbuję wczytać i zastanowić czy czegoś się nie dopatrzę

Adamm: EX jest źle

Adamm: prawdopodobieństwa obliczone dobrze

iteRacj@: a jak powinno być?

Adamm: powinnaś prawdopodobieństwa mnożyć przez wartość zmiennej losowej, a przemnażasz je przez długość krótszych z łuków

a7: niew eim czy o to chodzi, ale w mianowniku jest 11 razy 12

Adamm: mam nadzieję że rozumiesz, mimo że napisałem to trochę nie po polsku

iteRacj@: @a7to 12 sie skróciło, zostało w mainowniku 11 @Adammto mnie zastanowiło, dlaczego wartością oczekiwaną jest taki krótki łuk

Adamm: to co napisałaś, to E(2π−X)=2π−E(X)

Adamm: Więc nie wszystko stracone, można liczyć i tak

iteRacj@:

	8π		16π
EX=2π(11/12*2/11+10/12*2/11+9/12*2/11+8/12*2/11+7/12*2/11+6/12*1/11)=2π		=
	11		11

	6π
w odpowiedziach		, może jest błąd
	11

Adamm: albo źle przepisałaś treść

iteRacj@: sprawdziłam jeszcze raz treść i odpowiedź, przepisane prawidlowo (zresztą zadanie z matury)

	6π
ale odpowiedź		to za mało jak się wybiera dłuższy łuk
	11

a7: czy można prosić o "tok myślenia" przy pisaniu EX? dlaczego 1/12 itd wartości prawdopodobieństw rozumiem

iteRacj@: ten pierwszy zapis EX=2π(1/12*2/11+2/12*2/11+3/12*2/11+4/12*2/11+5/12*2/11+6/12*1/11) to mój błąd, tak jak Adamm napisał 23:44 powinny być mnożone wartości zmiennej losowej czyli EX=2π(11/12*2/11+10/12*2/11+9/12*2/11+8/12*2/11+7/12*2/11+6/12*1/11)

a7: no tak, w końcu to zrozumiałam, a jescze mam pytanie czy ten łuk AG trzeba uwzględniać, pytanie może głupie?

a7: ale chodzi mi o to że te dwa łuki są równe

Adamm: nie rozumiem pytania

a7: tak, to było przekombinowanie, sorry zapomniałam jak się liczy wartość oczekiwaną i dlatego sorry

Adamm: W porządku. Pytałaś się o P(X=π). Iteracja jako swoją przestrzeń zdarzeń przyjęła cięciwy od A do innego punktu.

	1
Wchodzi tutaj prawdopodobieństwo klasyczne, i mamy P(X=π)=
	11

a7: tak rozumiem pradwopodobieństwo,a le zmyliła mnie treść zadania bo tam było największego z łuków a nie wiekszego z łuków i chciałam przekombinować, że może łuki równe się pomija czy coś takiego, tak jak mówię zapomniałam że w wartości oczekiwanej bierzemy wszystkie wartości zmiennej i mnożymy razy ich prawdopodobieństwa, także stąd moje niezrozumiałe pytanie, dzięki

iteRacj@: dziekuję za pomoc i podpowiedzi