całka biegunowa xxx: ∫∫(y²−x²) dla obszaru √3≤x²+y²≤y D Policzyłem promien: √3cosφ≤r≤sinφ Jak poradzić sobie z kątami?

Adamm: dobrze przepisany obszar? tam chyba powinno być x√3

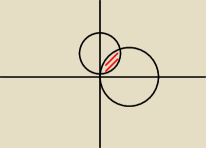
PW: Coś mi się zdaje, że rysunek nie jest poprawny. x²+y²≥√3 i x²+y²≤y

	1		1
x2+y2−y=x2+(y−		)2−		,
	2		4

obszar jest więc zdefiniowany jako zbiór par (x, y), dla których

	1		1
x2+y2≥√3 i x2+(y−		)2≤
	2		4

xxx: Tak,pomyliłem się.Powinno byc x√3

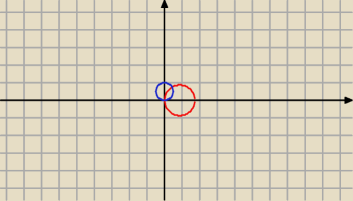
Adamm: sprawdzasz kiedy √3cosφ≤sinφ, sinφ≥0 cos(π/6)cosφ−sin(π/6)sinφ≤0, 0≤φ≤π cos(π/6+φ)≤0 π/2≤π/6+φ≤3π/2 φ∊[π/3, π]

Adamm: I źle zaznaczyłeś obszar na rysunku