Okrąg opisany w trójkącie Hubik: Punkt A(7,−1) jest wierzchołkiem trójkąta równoramiennego, w którym AC = BC. Okrąg wpisany w trójkąt ABC ma równanie x²+y²=10 Oblicz współrzędne wierzchołków B i C tego trójkąta. Proszę o pomoc ponieważ za każdym razem wychodzi mi zły wynik

Blee: to pokaż jak liczysz ... sprawdzimy

hubik: r=√10 A>r y=a(x−7)−1 ax−y−7a−1=0 A= a B=(−1) C=(−7a−1)

	|a*0−1*0−7a−1|
√10=
	√a2+1

√10*√a²+1=|−7a−1| 10(a²+1)=(−7a−1)² 10a²+10=49a²−14a+1 −39a²+14a+9 Δ=14²−4*−39*9 Δ=1600 √Δ= 40

	9
a1 =
	13

	1
a2 = −
	3

i następnie wyliczam proste z tego, które są złe...

sushi:

Mila: Jakie są odpowiedzi? Policzyłam, to wyślę.

Blee: błędnie wyliczone a₁ i a₂ a błąd zaczyna się tutaj: (−7a −1)² = 49a² + 14a + 1 bo (−7a−1)² = (7a+1)²

Blee: więc

	9
a1 = −
	13

	1
a2 = +
	3

sushi: 10a²+10=49a²+14a+1

hubik: Mila nie ma odpowiedzi Nauczyciel po prostu zadał nam to na lekcji

hubik: Dobra mam już policzone proste ale niestety to jedyne co umiem XD Nie za bardzo wiem jakich wzorów teraz użyć i co policzyć. Pomożecie?

Mila: Skonsultuj treść z koleżanką.

hubik: Nie rozumiem drugiego punktu...

	1
W sensie dlaczego tam jest x2 + (		x)2=10
	7

	1
gdy w pierwszym punkcie wyliczyliśmy że y = −		x
	7

i jak nagle powstał √5

hubik: Wszystko się zgadza, po prostu jestem głupi i nie umiem liczyć Dobrze że mam ciebie

Mila: Najważniejsze, że dochodzisz do prawdy, to zapamiętasz. Ja też mogę się mylić Trzeba pytać. Zapytałeś koleżanki lub kolegi o treść?

hubik: To zadanie polegało jedynie na wyliczeniu tego trójkąta. Nauczycielowi chciało się nas pognębić i zadał nam takie zadanie z głowy. Tylko masz i licz XD Dlaczego ja mam matematykę rozszerzoną...

Mila: Nie narzekaj. Trochę żmudnych rachunków nikomu nie zaszkodzi. Powodzenia w dalszych zmaganiach z królową nauk.

Basia: Zadanie z tegorocznej matury rozszerzonej. Rozwiązań w sieci jest pełno.

Mila: Dziękuję Basiu, okazało się w dodatku, że rozwiązałam od pewnego momentu inne zadanie Pozdrawiam.

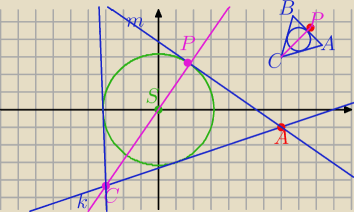
Mila: W treści zadania ( matura 2018) pisze dodatkowo, że obie wsp. C są ujemne. |AC|=|BC| 1) prosta AS:

	1
y=−		x
	7

2) Proste AB i AC: Odległość S=(0,0) od prostych równa R=√10 y=ax+b i b=−1−7a y=ax−1−7a⇔ ax−y−1−7a=0 U{|a*0−0−1−7a|}{√a²+1=√10⇔ |1+7a|=√10*√a²+1 /² 1+14a+49a²=10a²+10 39a²+14a−9=0

	1		9
a=		lub a=−
	3		13

	1		10
AC: y=		−
	3		3

	9		50
AB: y=−		x+
	13		13

======================= 3) AB − podstawa Δrównoramiennego P− punkt styczności okręgu z podstawą. x²+y²=10 i y=−U{9}{13)x+U{50}{13) stąd

	9		13
P=(		,		) − środek AB
	5		5

B=(x_b,y_b)

9		7+xb		13		−1+yb
	=		i		=		⇔
5		2		5		2

B=(−3,4; 6,2) 4) prosta PC ⊥AB przechodzi przez punkty P i S

	13
y=		x
	9

	13		1		10
C: y=		x i y=		x−
	9		3		3

	13
x=−3, y=−
	3

	13
C=(−3,−		)
	3