hmm michas: Rozpatrujemy wszystkie trapezy równoramienne, w których długość krótszej podstawy i długości ramion są równe 5 . Oblicz długość dłuższej podstawy tego z rozpatrywanych trapezów, który ma największe pole.Oblicz to pole. Mozna za pomocą samej a obliczyc bo np dajmy na to ze nie wpadne na taki pomysl zeby obliczyc ten odcineczek a−5/2 rozumiecie?

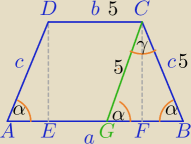
Mila: Można, ale to chyba będzie trudniej dla Ciebie. CG||AD

	π
α∊(0,		)
	2

γ=180−2α sinγ=sin(180−2α)=sin2α P=P_trapezu=P_AGCD+P_ΔGCB

	1
P(α)=52*sinα+		*5*5*sinγ
	2

	1
P(α)=25*(sinα+		sin(2α) )
	2

P'(α)=25*(cosα+cos(2α)) P'(α)=0⇔cosα+cos2α=0 i α− kąt ostry 2cos²α+cosα−1=0 cosα=t, t∊(0,1) 2t²+t−1=0

	1
t=−1∉D lub t=
	2

	1
cosα=		⇔α=60o i funkcja P(α) ma maksimum lokalne dla α=60o
	2

(zbadaj znak pochodnej)

	√3
P=25*(sin60+0.5 sin 120o)=25*3*		⇔
	4

	75√3
P=
	4

=========== Może Eta poda jeszcze inne rozwiązanie.

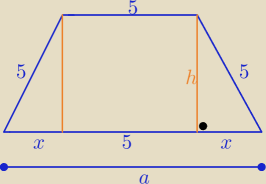
Eta: 2 sposób: ( bez trygonometrii) a=2x+5

	a+5
z tw. Pitagorasa : h=√25−x2 , x ∊(0,5) , P=		*h
	2

P(x)= (x+5)*√25−x²

	(x+5)*x
P'(x)= √25−x2−
	√25−x2

P^'(x)=0 ⇒ ....... 2x²+5x−25=0 ⇒ x=2,5 ....... zbadaj znak pochodnej dla x=2,5 to a=10 i h= √75/4 ⇒ h=2,5√3 P=................

	75√3
P=
	4

============