uzasadnienie pabloo: Wyznacz te wartości parametru k dla których równanie x³−9x=k w przedziale <0;3> ma dwa rozwiązania.

Jerzy: 1) Δ > 0 2) 0 < x_w < 3 3) f(0) ≥ 0 4) f(3) ≥ 0

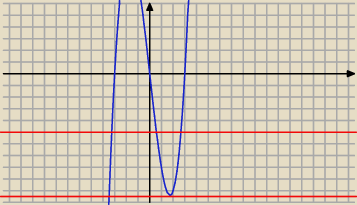
PW: Funkcja f(x)=x³−9x ma trzy miejsca zerowe: −3, 0, 3 (niebieski wykres) Równanie f(x)=k ma dwa rozwiązania na <0, 3>, jeżeli k∊(f_min, 0>. Przykładowe dwie czerwone proste o równaniach y=−5 oraz y=f_min pokazują jedną z "dobrych k" oraz ograniczenie z dołu zbioru "dobrych k". Wystarczy znaleźć minimum lokalne funkcji k i odpowiedź gotowa.

PW: Korekta: W ostatnim zdaniu powinno być " minimum lokalne funkcji f ".