równanie bartek: Wykaż że jeżeli równanie x⁴+mx²+n=0 ma cztery różne rozwiązania tworzące ciąg arytmetyczny to 100n=9m²

Blee: Skoro to maja byc ROZNE miejsca zerowe tworzace ciag arytmetyczny to wiemy ze sa postaci: a+r a −a −a−r (Patrz wzory Viete'a) Posilkujac sie wzorami Viete'a dochodzimy do wskazanej rownosci

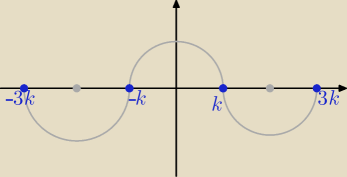
Eta: Prawa strona jest funkcją parzystą więc rozwiązania są symetryczne względem osi Oy zatem (x−k)(x+k)(x−3k)(x+3k)=0 ⇒ (x²−k²)(x²−9k²)=0 ⇒ x⁴−10k²+9k⁴=0 m= −10k² i n=9k⁴ m²=100k⁴ i otrzymujesz tezę : 100n=9m² ===========