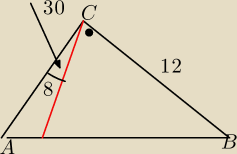
Oblicz długosć odcinka CD i promień okręgu opisanego na trójkącie ABC Marcin: W trójkącie ABC mamy dane: |AC| = 8, |BC| = 12 oraz |ACB| = 120°. Przez wierzchołek C poprowadzono prostą prostopadłą do boku BC. Przecięła ona bok AB w punkcie D. Oblicz: a) długość odcinka CD b) promień okręgu opisanego na trójkącie ABC.

Krzysiek60:

Marcin: Ale skoro prowadzimy prostą prostopadłą do boku BC to ta czerwona kreska nie powinna być pod kątem prostym do AB? i skąd wiem to, ze dzieli mi się to na kąty 90 i 30? Może to głupie i proste pytanie, ale własnie to jest dla mnie przeszkodą

Krzysiek60: Wedlug mnie nie .Pisze do boku BC

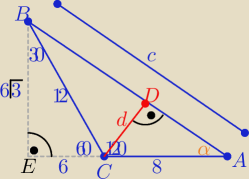
Eta: 1/ w ΔECB : |EB|=h=6√3 , |EC|=6 to c=√6√3)²+14² ⇒ c=4√19 Z podobieństwa trójkątów EAB i CAD z cechy (kkk)

d		c		12√57
	=		⇒ d=
6√3		8		19

	abc
2/ dla ΔABC : R=
	4P

	1
P(ABC)=		*6√3*8 ⇒ P=......
	2

	12*8*c
R=		=.....................
	4P

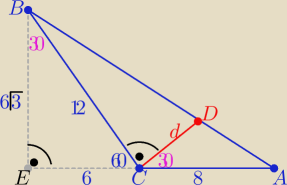
Eta: Poprawiam zgodnie z treścią 1/ P(ABC)= ..= 24√3

	1		1
P(ACD)=		*8*d*sin30o = 2d i P(DCB)=		*12*d = 6d
	2		2

2d+6d=24√3 ⇒ d=3√3 2/ identycznie jak podałam wyżej.......

Eta: A Marcin pewnie już ... poszedł na spacer

Marcin: Zrobiłem te zadanie samemu i nie wchodziłem już tutaj, myslalem, ze bedzie dobrze... Jednak mialem błąd i teraz poprawiam. Dziękuję

Eta: No i tak trzymaj

Marcin: R mi wyszlo 3 √57/3

Eta:

	4√57
R=
	3