Napisz równanie: Nenya: Napisz równanie: a. wysokości trójkąta ABC, opuszczonej z wierzchołka C na bok AB, b. środkowej CS jeśli A=(−3,−1), B=(−1,5), C=(3,1)

iteRacj@: 1/ wyznacz współczynnik kierunkowy prostej przechodzącej przez pkt A i B

	yB−yA		5−(−1)
aAB=		=		=3
	xB−xA		−1−(−3)

2/ wyznacz współczynnik kierunkowy prostej prostopadłej do prostej AB

	−1
aCD*aAB=−1 aCD=
	3

3/ podstaw współrzędne pktu C=(3,1) do równania prostej o współczynniku kierunkowym a_CD y−y_C=a_CD*(x−x_C)

	−1
y−1=		*(x−3)
	3

Nenya: nie rozumiem

iteRacj@: który podpunkt jest niezrozumiały?

Nenya: w sumie wszystko bo nie powinno się od jakies wysokosci zaczynac?

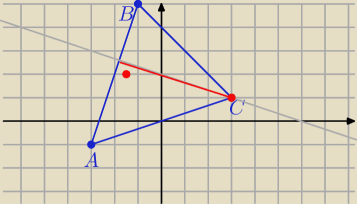Janek191: A = ( − 3, − 1) B = ( − 1, 5) więc współczynnik kierunkowy prostej AB jest równy

	5 − (−1)		6
a =		=		= 3
	− 1 − (−3)		2

Prosta prostopadła do pr AB ma równanie:

	1
y = −		x + b
	3

Ma przechodzić przez c = ( 3, 1), więc

	1
1 = −		*3 + b ⇒ b = 2
	3

Odp.

	1
y = −		x + 2
	3

==============

Janek191: b) S − środek AB, więc

	−3 − 1		− 1 + 5
S = (		.		) = (−2, 2)
	2		2

Teraz napisz równanie prostej CS

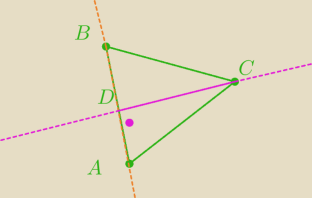iteRacj@: Szukam równania prostej zawierającej wysokość opuszczoną z wierzchołka C na bok AB, na tym skończę obliczenia. Ta prosta (oznaczam ją CD) jest prostopadła do boku AB, bo wysokość tworzy z bokiem AB kąt prosty. 1/ Korzystam ze wzoru na współczynnik kierunkowy prostej przechodzącej przez dwa podane punkty u nas A i B. Współczynnik kierunkowy wystarczy do obliczeń, nie muszę znajdować równania prostej AB. 2/ Korzystam ze wzoru na zależność pomiędzy współczynnikami kierunkowymi prostych prostopadłych. Znajduję współczynnik kierunkowy prostej prostopadłej do danej prostej (u nas AB). 3/ Takich prostych jest nieskończenie wiele, muszę wybrać tę, która przechodzi prze pkt C, dlatego do wzoru podstawiam jego współrzędne. Moje obliczenia musisz jeszcze powymnażać i uporządkować i będziesz mieć równanie prostej zawierającej wysokość opuszczoną z wierzchołka C na bok AB