Optymalizacja_funkcje pochodne Marta: Zadania optymalizacyjne. Pomocy! 3 zadania do ogarnięcia: 1. Drut o długości "a" podzielono na dwie części. Z pierwszej wykonano szkielet sześcianu a z drugiej szkielet z prostopadłościanu o podstawie kwadratowej i polu ściany bocznej dwukrotnie większym niż pole podstawy. W jakiej proporcji należy podzielić drut aby suma objętości tych brył była najmniejsza? 2. Wyznacza w zależności o parametru "a" współrzędne punktu należącego do wykresu funkcji f(x)=x² i leżącego najbliżej punktu P (0,a) 3. Rozważmy wszystkie trójkąty równoramienne o obwodzie 2p. Obracając te trójkąty o wokół podstawy otrzymujemy bryły o różnych objętościach. Oznaczamy przez V₁ największą z tych objętości. Obracając dane trójkąty wokół osi symetrii, otrzymujemy stożki o różnych objętościah. Niech V₂ będzie największą z nich. Oblicz V₁ : V₂

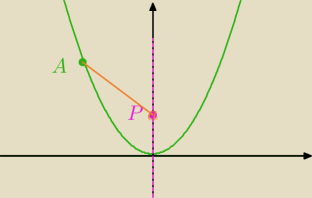
iteRacj@: 2. Wyznacz w zależności o parametru a współrzędne punktu A należącego do wykresu funkcji f(x)=x² i leżącego najbliżej punktu P=(0,a) szukany pkt oznaczamy A, ma on współrzędne A=(x, x²) obliczasz odległość punktów A i P |AP|=√(x−0)²+(x²−a)²=√x⁴−x²(2a−1)+a² pkt A bedzie leżeć najbliżej punktu P, gdy odległość |AP| będzie najmniejsza czyli wtedy kiedy funkcja pod pierwiastkiem będzie mieć najmniejszą wartość f(x)=x⁴−x²(2a−1)+a² teraz musisz znaleźć minimum (minima) tej funkcji, więc trzeba obliczyć jej pochodną

Marta: A mam dwie niewiadome, wiec jak kto potraktować ?

iteRacj@: a to jest parametr, zmienną jest x (dlatego zapis f(x)) parametr jest stałą, traktujesz go tak jak liczbę przy liczeniu pochodnej