w trojkacie ABC mamy dane AB=4 wifik: W trójkącie ABC mamy dane: |AB| = 4, |BC| = 4 3 i |BAC| = 60°. Oblicz: a) pole trójkąta ABC b) promień okręgu wpisanego w trójkąt ABC; wynik zapisz w postaci a +b √c Jak na razie zrobilem punkt a i wyszlo mi 8 √3 w b nie mam pojecia jak to zrobic...

Ice Tea: Skorzystaj z tw. cosinusów, dzięki niemu możesz obliczyć trzeci bok. Oblicz pole z wzoru Herona, a następnie skorzystaj z tego: P = rp , gdzie P to pole trójkąta a p to połowa obwodu, i możesz wyznaczyć promień okręgu wpisanego.

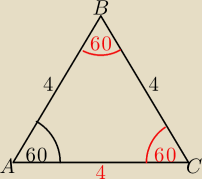
Bogdan: a może tak?

wifik: czyli po kolei: a²=4²+(4{3})²−2*4*4{3}*cos90 z tego wyszlo ze a=√70 czy to dobry wynik?

Bogdan: chyba, że |BC| = 4√3, ale tego zapisu nie widać

wifik: tak, 4 √3, moj blad, pierwszy raz tego uzywam

Bogdan:

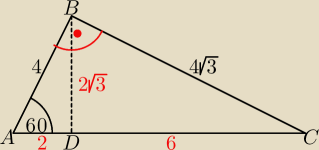
	1
wtedy |AD| =		*4 = 2 i |BD| = 2√3, |DC| = √48 − 12 = 6
	2

|AB|² + |BC|² = |AB|², trójkąt ABC jest prostokątny

wifik: co mam dalej zrobic? nie moge zalapac tego, z wzoru herona tez mi nie wychodzi

wifik: ktos pomoze?:(

iteRacj@:

	1		1
trójkąt jest prostokątny, więc pole PABC=		|AB|*|BC|=		*4*4√3
	2		2

iteRacj@: Promień okręgu wpisanego możesz wyznaczyć ze wzoru podanego przez Ice Tea P_ABC = rp to jest wzór dla dowolnego trójkąta

	4+8+4√3
8√3=r
	2

	a+b−c
lub skorzystać ze specjalnego wzoru dla trókjąta prostokątnego r=
	2

	4+4√3−8
r=
	2