całka podwójna kkk: Za pomocą całki podwójnej oblicz pole obszaru ograniczonego krzywymi: y=−x²+4, y=3√x, x=0

Blee: A po co całka podwójna skoro lecisz na płaszczyźnie

Jerzy: Ma takie polecenie.

kkk: No ja wiem, że z tego wyjdzie pojedyncza, ale taką mam treść zadania, a mógłbyś/mogłabyś mi to rozpisać, bo mi to nie wychodzi

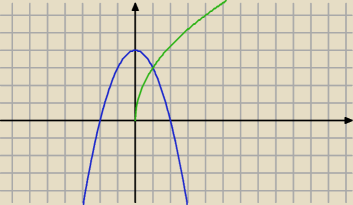
Jerzy: Dzielisz na dwa obszary. P = ₀∫¹₀∫^3√xdydx + ₁∫²₀∫^−x2+4dydx

kkk: tak zrobiłam tylko z 1 obszaru wychodzi mi 2 a z drugiego 5/3 a w odpowiedziach mam 5/3 więc nie wiem czy zle liczę całkę czy jest bład w odpowiedziach

Jerzy: Pokaż,jak to liczysz.

kkk: z pierwszej całki będzie 2x³/2 (2 do 3/2) w granicach od 0 do 1 więc po podstawieniu wychodzi 2. A w drugiej całce wychodzi [−1/3x³+4x] w granicach od 1 do 2 więc po podstawieniu wyjdzie 5/3

kkk: czyli ma wyjść 2+5/3=11/3 czy tak jak jest w odp 5/3, który wynik jest poprawny?

kkk: ?

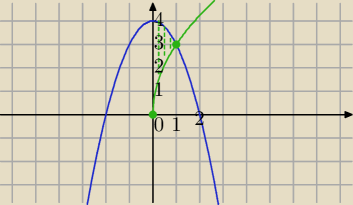
Mila: y=−x²+4, y=3√x, x=0 ₀∫¹_y=3√x∫^−x2+4 dy dx= =₀∫¹[ y]_3√x^−x2+4dx=

	1		2
=0∫1(−x2+4−3√x) dx=[−		x3+4x−3*		x3/2]01=
	3		3

	1		1		2		5
=−		+4−2=2−		=1		=
	3		3		3		3

kkk: dziękuję bardzo