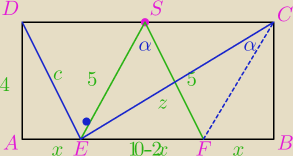
Okrąg matma po nocach: Dany jest prostokąt ABCD o bokach długości: |AB| = 10, |AD| = 4 oraz okrąg o środku S (Sśrodek CD) i promieniu |SC|. Okrąg ten przecina bok AB w punktach E i F. Oblicz pole czworokąta CDEF. Kąt DEC jest kątem prostym, bo opartym na średnicy okręgu. c²=4²+x² ΔAED 10²=c²+z²−2cz ΔDEC 10²=z²+c²−2cz*sinα ΔEFC (10−2x)²=5²+5²−2*5*5*cosα ΔEFS => sin²α+cos²α=1 Mam 4 niewiadome i 4 równania, więc jestem w stanie obliczyć wszystko, ale w kluczu jest bardzo krótko; wyliczenie z trójkąta DEC 4²=x*(10−x), niestety nie wiem skąd się to wzięło, czy ktoś mógłby mi powiedzieć?

matma po nocach: Tam oczywiście powinno być cosα przy tw. cos., a dwa ostatnie równania z tw cos lekko wymieszałem, ale chodzi o rozpisanie, bo zostało to już wyliczone.

matma po nocach: Więc też jedynka trygonometryczna nie jest potrzebna

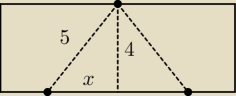
Blee: ile wynosi 'x' (tw. Pitagorasa) I dalej chyba już sobie poradzisz, prawda ?!

matma po nocach: Jejku jestem ślepy, dziękuję

Blee: Niestety ... podszedłeś/podeszłaś do tego zadania 'od dupy strony' Bo jak widzisz − zadanie jest na 2 minuty roboty

Blee: a co do DEC (korzystam z Twoich oznaczeń) −> c² = 4² + x² z² = (10−x)² + 4² c² + z² = 2*4² + x² + (10−x)² więc: 2*4² + x² + (10−x)² = 10² 2*4² + x² + 100 − 20x + x² = 100 2*16 + 2x² − 20x = 0 i z tego masz x=2 lub x = 8 (druga odpowiedź oczywiście odpada).

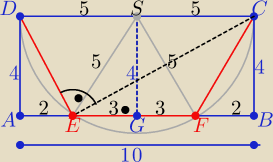
Eta: P(ABCD)= 40 , P(ΔAED)=P(ΔCBF)= 4 P(CDEF)= 40−2*4=32