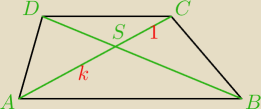
Trapez matma po nocach: W nierównoramiennym trapezie ABCD (AB || CD) przekątne AC i BD przecinają się w punkcie S takim, że AS : SC = k : 1. Oblicz stosunek pola trójkąta CDS do pole trapezu ABCD. P ΔASD= P ΔCDS * k P ΔBCS= P ΔCDS * k ponieważ mają tą samą podstawę i wysokość Δ CDS ~ Δ ABS z tw. o 2 pr. równ, przeciętych 3 I krok którego nie rozumiem jest: P ΔABS= P ΔCDS * k² Mógłby mi ktoś rozjaśnić dlaczego k²? Jedyne wyjaśnienie to to, że z podobieństwa.

Krzysiek60: Stosunek pol figur podobnych jest rowny kwadratowi skali podobienstwa

matma po nocach: Rzeczywiście, dziękuję

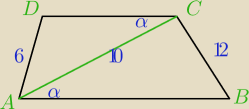
matma po nocach: Dany jest trapez ABCD (AB || CD ; |AB|>|CD|) w którym dane są: |AD|= 6, |BC|= 12, |AC|= 10, ∢BAC = ∢ACD = 30°. Oblicz pole trapezu ABCD. α= 30^o Z twierdzenia cosinusów obliczam kolejno AB oraz CD, które wynoszą AB = 20 CD = 5

	12		20
Z cechy BKB wnioskuję, że ΔABC ~ ΔADC (30o ;		=		).
	6		10

I tu koniec, jak mam obliczyć h? Nie mogę porównać wysokości przy wierzchołku C, bo nie znam kąta przy wierzchołku B? Pewnie, mógłbym użyć wzoru na pole trójkąta posiadając sinus kąta, podstawić to do wzoru na zwykłe pole trójkąta i wyliczyć h, ale w rozwiązaniach jest szybki sposób; zauważenie cechy KKK (nie BKB), obliczenie podstaw z podobieństwa i obliczenie h z trygonometrii? Jak wygląda to zauważenie KKK i określenie długości podstaw + wysokości? Kompletnie tego nie widzę.

Krzysiek60: Moze np tak policzyc pole trazpezu P_tr= P_ΔBAC+P_ΔACD Masz wszystkie dane zeby policzyc P_Δ= 0.5 a*b*sinα(ogolnie