Podobieństwo trójkątów Nel: Dane jest koło i punkt P należący do wnętrza koła. Przez punkt P prowadzimy średnicę AB dowolną cięciwę CD. Wykaż, że ∆APC jest podobny do ∆BPD

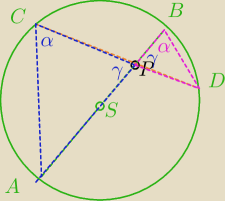
iteRacj@: skorzystaj z tego, że <CPA i <BPD są kątami wierzchołkowymi a <ACP i <ABD oraz <CAB i <CDB są kątami wpisanymi opartymi na tych samych łukach

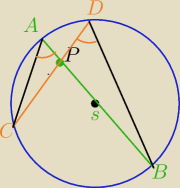
Mila: 1) ∡A=∡D − jako kąty wpisane w okrąg oparte na tym samym łuku 2) ∡APC=∡BPD − jako kąty wierzchołkowe 3)∡C=∡B − suma kątów w Δ.⇔ ∆APC jest podobny do ∆BPD− cecha kkk