optymalizacja pablo: W ostrosłup prawidłowy sześciokątny, którego krawędź podstawy ma długość 10, a wysokość ma długość 6√3, wpisujemy prostopadłościany w ten sposób, że jedna podstawa prostopadłościanu zawiera się w podstawie ostrosłupa, a wierzchołki drugiej podstawy należą do krawędzi bocznych ostrosłupa. Oblicz objętość prostopadłościanu o największym polu powierzchni bocznej.

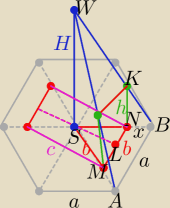
Eta: Wymiary prostopadłościanów: b,c,h

	b√3
ΔMSN równoboczny o boku b to c= 2|SL|= 2*		⇒ c=b√3
	2

|BS|=a= |SN|+NB| ⇒ |NB|=x = a−b , dla a=10 to x= 10−b , b∊(0,10) Z podobieństwa trójkątów SBW i NBK z cechy (kkk)

H		h		6√3
	=		⇒ h=		(10−b)
a		x		10

pole boczne prostopadłościanu: P_b= 2bh+2ch

	6√3
to P(b)=		(10−b)*b(1+√3)
	5

P^'(b)=0 ⇒ ........ b=5 wykresem jest parabola ramionami do dołu więc osiąga wartość największą dla b = 5 to c= b√3=5√3 i h=....=3√3 V=cbh =5√3*5*3√3 = 225 [j²]

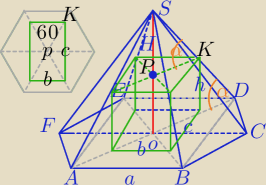
Mila: a=10 H=6√3 Prostopadłościan wpisany w ostrosłup sześciokątny P_b=2b*h+2c*h ΔSPK∼SOD |OD|=a

H−h		H
	=		gdzie |PK|=b, c=b*√3
|PK|		a

6√3−h		6√3
	=
b		10

	3√3
h=		*(10−b)
	5

P_b=2b*h+2b√3*h=2b*h*(1+√3)

	6√3
Pb(b)=		*(1+√3)*(10b−b2)
	5

b_w=5 c=5√3

	3√3
h=		*(10−5)=3√3
	5

V=5*5√3*3√3=25*3*3=225 ======================== Napisz, czy taka jest odpowiedź.

pablo: tak, przepraszam , taka odpowiedz, dziekuje slicznie

Mila: