Liczenie kąta między bokami trójkąta Alucarddo: W trójkącie ABC dane są (współrzędne wektorów) AB = [ 1,3 ] i CA = [ −√2, 2√2] oraz kąt BAC = α. Trzeba obliczyć α. Ktoś by mi to wytłumaczył ? Myślałem nad poprowadzeniem wysokości dzielącej AB na pół, po czym policzenie tg α ale coś mi nie wyszło

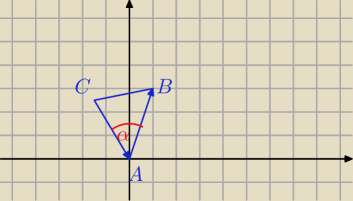
Janek191: → AB = [ 1, 2] → AC = [ − √2, 2√2] więc I AB I = √1 +3² = √10 I AC I = √ 2 + 8 = √10

	1*(−√2) + 2*2√2		3√2
cos α =		=
	√10*√10		10

Janek191: Pomyłka Zły rysunek i reszta.

Alucarddo: Więc czekam dalej

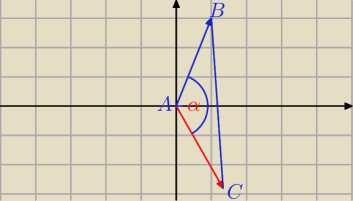
Janek191: → AB = [ 1, 3] → AC = [ √2. − 2√2] więc I AB I = √10 I AC I = √10

	1 *√2 − 3*2√2		− 5√2
cos α =		=		= − 0,5√2
	√10*√1		10

α = 135^o ===========