romb Dawid: Dwa zadania których nie potrafię rozwiązać 1)Kąt ostry rombu ma miarę 30⁰, a suma długości przekątnych jest równa 20 cm Wiedząc że tg30⁰=2−√3,oblicz pole tego rombu 2) Pole rombu jest równe 156 cm².Wysokość rombu ma długość 12 cm. Oblicz sumę długości jego przekątnych .

sushi:

	√3
tg 30o=		, a nie tak jak podałeś w zadaniu
	3

Bogdan: tg15^o = 2 − √3

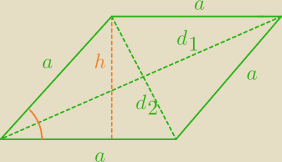
iteRacj@: 2/ zastosuj dwa wzory na pole rombu P=a*h=a²*sin α 156 cm²=a*12 cm → a= 13 cm 156 cm²=(12 cm)²*sin α z tego równania wylicz sin α z tw. cosinusów oblicz krótszą przekątną z kolejnego wzoru na pole rombu wylicz dłuższą przekątną

	1
P=		*d1d2
	2

i teraz je zsumuj

iteRacj@: * 156 cm²=(13 cm)²*sin α

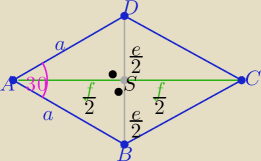
Eta: 1) można rozwiązać .. bez informacji o tg15^o=2−√3

	fe
P=a2*sin30o ⇒ 8P=4a2 i P=		⇒ 4P=2fe
	2

z tw. Pitagorasa w ΔABS: f²+e²=4a² ⇒ (f+e)²−2fe=4a² ⇒ 20²−4P=8P ⇒

	100
P=		cm2
	3

=========

Eta: 2/ podobnie

	fe
P=a*h ⇒ a=13 i P=		⇒ 2fe=4P
	2

f²+e²=4a² ⇒ (f+e)²−2fe= 4*169 ⇒ (f+e)²= 4*169+4P ⇒(f+e)²=........ f+e= 10√13 cm =========