Dziedzina? miram : jak mam wyznaczyć dziedzinę,gdy pood mianownikiem mam 4x³−8x²−x+2

Krzysiek60: 4x²(x−2)−1(x−2)≠0 (x−2)(4x²−1)≠0

miram : Wyszło mi 2 i −2

Krzysiek60: 2 zgoda ale (−2) 4x²−1≠0 (2x+1)(2x−1)≠0 to x≠ i x≠

miram: skoro mam 4x²− 1 i zostaje mi x² to nie biorę pod uwagę zarówno liczby dodatniej jak i ujemnej?

miram: dobra nie ważne już widze, że może być tylko 2

Krzysiek60: 4x²−1 rozkladam ze wzoru skroconego mnozenia a²−b²= (a+b)(a−b) wiec 4x²= (2x)² 1= 1²

	1		1
4x2−1= (2x)2−12= (2x+1)(2x−1) ≠0 ⇔gdy 2x−1≠0 ⇒x≠		i 2x+1≠0 ⇒x≠−
	2		2

	1		1
Df= ℛ\{−		,		,2}
	2		2

Mila: Źle to interpretujesz. Rozwiązujesz równanie: 4x³−8x²−x+2=0 4x²*(x−2)−(x−2)=0 (x−2)*(4x²−1)=0⇔ (x−2=0 lub 4x²−1=0

	1
x=2 lub 4x2=1⇔x2=
	4

	1		1
x=2 lub x=		lub x=−
	2		2

	1		1
D=R\{−		,		,2}
	2		2

Mila: Już się nie wtrącam, bo widzę, że Krzysiek jest pomocny. Pozdrawiam

Krzysiek60: Milu Przed chwila mialem pisac zeby wykorzystala Twoja pomoc tylko zagladnalem na post sikorki czy policzyla

miram: https://pl-static.z-dn.net/files/da3/0d3aa0e2d34583d1fc8a53af6256ce57.jpg

miram: No więc zrobiłam mam nadzieję,że dobrze

Krzysiek60: Musze sobie skrecic glowe zeby odczytac Poza tym jesli piszesz np x−2≠0 to muszisz byc konsekwentna do konca i x≠2 a nie x=2 To samo drugi zapisz

Mila: Popatrz na moje rozwiązanie 19:01 i zobacz błąd u siebie.

Mila: Dla jakiej liczby masz obliczyć wartość?

miram: dla liczby 0,5

Mila: miram tam w linku w mianowniku jest: 4x³−8x²+x+2 a Ty podałaś o 17:37 4x³−8x²−x+2 To jaki ma być ten mianownik? Bo dla 4x³−8x²+x+2 będzie inna dziedzina niż dla: 4x³−8x²−x+2

Krzysiek60: I pomijac to ze pewnie pomylka W linku 4x²−1≠0 4x²=−1

	1
x2=−
	4

	1		1
x= −		lub		Toz to herezja dlaczego ?
	2		2

Mila: Prosiłam, aby szukała błędu.

miram : mila: Czyli rozumiem,że minus nie moze być

Mila: Napisz porządnie treść, a konkretnie jaki ma być mianownik, to wszystko ustalimy.

miram: wyślę zdj sprawdzianu, ponieważ mam do w dwóch jakościach

miram: go*

Mila: Dobrze.

miram: http://files.tinypic.pl/i/00965/3bbj7g8a8eb3.jpg

Mila:

	x+2
f(x)=
	4x3−8x2−x+2

	1		1
D=R\{−		,		,2}
	2		2

	1
0.5=		nie należy do dziedziny funkcji
	2

wyrażenie nie sensu dla x=0.5 bo w mianowniku wychodzi 0, a przez zero nie wolno dzielić. Nie można obliczyć wartości tego wyrażenia dla x=0.5

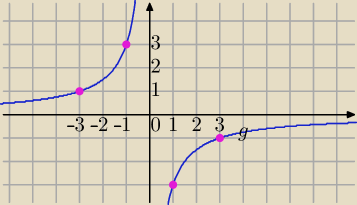
Mila: zad 6 Narysuj wykres funkcji:

	3
f(x)=−		+2
	x−1

1) Rysujesz wykres

	−3
g(x)=
	x

Punkty wykresu (1,−3), (3,−1) 2) przesuwasz o wektor [1,2] 1 jednostka w prawo i 2 jednostki w górę

	−3
otrzymujesz wykres f(x)=		+2
	x−1

narysuj na kartce i daj na wrzutę.

Mila: zadanie 1 a

9x		1
	, obliczyc wartość dla x=
12−4x		6

D: 12−4x≠0⇔12≠4x /:4 x≠3

	1		1   9*   6		9   6
w(		)=		=		=
	6		1   12−4*   6		4   12−   6

3   2		3		1		3		34
	=		: 11		=		:		=
2   12−   3		2		3		2		3

	3		3		9
=		*		=
	2		34		68