geometria analityczna qaz: Punkt A = (7, −1) jest wierzchołkiem trójkąta równoramiennego ABC, w którym AC = BC . Obie współrzędne wierzchołka C są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie x²+y²=10 . Oblicz współrzędne wierzchołków B i C tego trójkąta

sushi: rysunek zrobiony?

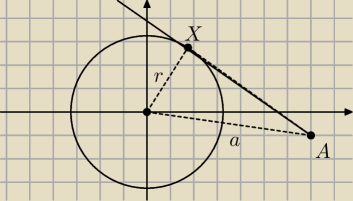
Blee: Pytanie pomocnicze −−− ile prosty stycznych do okręgu można poprowadzić z punktu leżącego poza tym okręgiem? Odpowiedź brzmi: dwa Wyznacz współrzędne punktu X (i analogicznego X' ). Wyznacz proste zawierające punkt X i A oraz X' i A. Wyznacz równanie prostej przechodzącej przez A i środek okręgu oraz wyznacz punkt A' −−− czyli punkt przecięcia tejże prostej z okręgiem w II ćwiartce. Wyznaczasz prostą styczną do tegoż okręgu w punkcie A'. Przecięcie się się tej prostej z tymi wyznaczonymi wcześniej wyznacza punkty B i C.