Całka podwójna srqt: Pomocy! Całki! Oblicz objętość bryły ograniczonej paraboloidą z=x²+y² i płaszczyznami z=x+y, x=0, y=0, z=0. Kompletnie nie mam pojęcia co z tym zrobić, większość zadań ogarniam.

Adamm: twój obszar całkowania to koło, o środku (1/2, 1/2) i promieniu √2/2 trzeba zastosować np. współrzędne biegunowe x=rcosα+1/2 y=rsinα+1/2

srqt: Właśnie głowię się i głowię, i nie potrafię wymyślić jak ten obszar całkowania uzyskać. Jak znalazłeś ten obszar?

Adamm: x²+y²≤x+y to mamy koło no to w sumie nie będzie koło jako takie, brakuje dolnego i lewego brzegu

Adamm: ja podzieliłbym obszar na 2 D₁={(x, y): x+y=1, x, y≥0} − trójkąt oraz D₂ − półkole

jc: x² + y² ≤ z ≤ x+ y x ≥ 0 y ≥ 0 x = 1/2 + r cos t y = 1/2 + r sin t x+y − x²−y² = 1/2 − (x−1/2)² − (y−1/2)² = 1/2 − r² V = ∫_−π/4^3π/4 dt ∫₀^1/√2 (1/2 − r²)rdr. + ∫₀¹ dx ∫₀^1−x [x+y − x²−y²] dy

srqt: Wyjdę pewnie na głupka, no ale cóż, mówią, że kto pyta, ten nie błądzi. Mógłbyś wytłumaczyć jakoś łatwiej skąd wcześniejsze stwierdzenie, że jest to koło o środku 1/2 i 1/2? x2+y2≤x+y <−−− ten moment rozumiem, z tym, że zazwyczaj zamiast nierówności robiłem tutaj równanie, ale znowu, dlaczego brakuje w tym kole brzegów? Jego promień to będzie √x+y? I wreszcie skąd nagle pojawił się trójkąt?

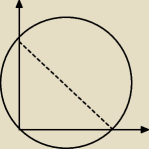
jc: Rysunek.

Adamm: narysuj sobie obszar całkowania, i spójrz na to co napisał jc

jc: W każdym punkcie inny promień

srqt: x² + y² ≤ z < −−− w jaki sposób to jest spełnione? Skoro bryłę ogranicza z=0, to jak x²+y² może być mniejsze niż 0? Gdzie mój błąd w rozumowaniu?

srqt: hmmm... Ta paraboloida znajduje się w tym wypadku nad osią OXYZ, prawda?

piotr: paraboloida z=x²+y² i płaszczyzna z=x+y przecinając się tworząc krzywą zamkniętą, której rzutem na płaszczyznę OXY jest okrąg: x² + y² = x + y ⇒ (x − 1/2)² + 2 (y − 1/2)² = 1/2

srqt: Dobra. Zrozumiane. Dzięki wielkie panowie, ratujecie życie!

srqt: Panowie* Mea culpa!

piotr: ** (x − 1/2)² + (y − 1/2)² = 1/2

piotr: https://www.wolframcloud.com/objects/e8f16909-33ac-49de-91ac-02783fd3132b