ile kół zmieści się w kole
house:
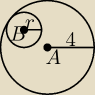
Chciałbym wiedzieć, ile wynosi promień koła stycznego do koła x
2+y
2≤16 oraz
prostych x=0 i y=0. Jest na to jakiś fajny sposób z poziomu liceum?
21 maj 20:56
iteRacj@:
czy w treści zadania chodzi o koła styczne zewnętrznie do koła o równaniu x2+y2≤16 ( i do
podanych prostych)?
21 maj 21:13
iteRacj@:
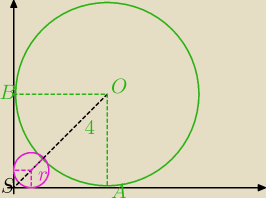
są dwa takie koła
tu na rysunku to o mniejszym promieniu r
|SO|=
√2*4
|SO|=4+r+
√2*r
czyli
√2*4=4+r+
√2*r i z tego łatwo wyliczysz
promień tego większego R spełnia równanie
√2*R=R+4+
√2*4
21 maj 21:26
iteRacj@:
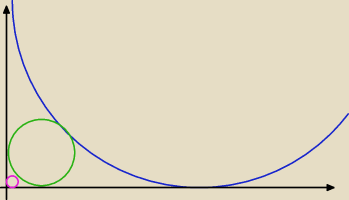
a tu widać to drugie większe koło i to małe
21 maj 21:30
house: Tak, chodzi o koła styczne do koła o równaniu x2+y2≤16 i do podanych prostych.
Super sposób, dziękuję.
21 maj 22:10
Blee:
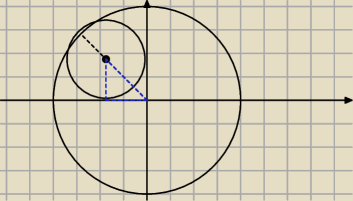
zacznijmy od tego, że środek tego okręgu leży na prostej y = x lub y = −x
mały niebieski trójkąt to trójkąt równoramienny o podstawie = 4−r i ramionach równych
(oczywiście r>0 i r<4)
z tw. Pitagorasa:
r
2 + r
2 = (4−r)
2
2r
2 = 16 − 8r + r
2
r
2 + 8r − 16 = 0
Δ = 2*64
21 maj 22:18
iteRacj@: 
no właśnie, nie narysowałam okręgu x
2+y
2≤16
21 maj 22:26
house: ehh no przecież, czemu nie widzę takich oczywistości

21 maj 22:28
house: @iteRacj@ tak czy inaczej schemat załapałem

21 maj 22:28
iteRacj@:
chociaż tyle pożytku,
zasugerowałam się zadaniem z tegorocznej matury
21 maj 22:31
house: faktycznie był jakiś dowód na podstawie, jeśli dobrze pamiętam
21 maj 22:32
iteRacj@:
@Blee dzięki !
21 maj 22:34
iteRacj@:
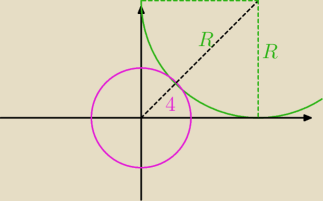
ale że nie odpuszczam kół stycznych zewnętrznie, to może jeszcze takie cztery koła o promieniu
R spełnią warunki zadania?
√2*R=4+R
21 maj 22:44
house: Jakby nie patrzeć spełniają, nie jestem widocznie zbyt precyzyjny
(w zamyśle miały być styczne wewnętrznie).
Ułożyłem takie zadanko, bo byłem ciekawy ile kół można by jeszcze ułożyć z wycinków
pól 16π−4*π(4√2 − 4)
2 
21 maj 23:00
house: *ile kół o promieniu 4√2 − 4...
21 maj 23:02
 Chciałbym wiedzieć, ile wynosi promień koła stycznego do koła x2+y2≤16 oraz
prostych x=0 i y=0. Jest na to jakiś fajny sposób z poziomu liceum?
Chciałbym wiedzieć, ile wynosi promień koła stycznego do koła x2+y2≤16 oraz
prostych x=0 i y=0. Jest na to jakiś fajny sposób z poziomu liceum?
 są dwa takie koła
tu na rysunku to o mniejszym promieniu r
|SO|=√2*4
|SO|=4+r+√2*r
czyli √2*4=4+r+√2*r i z tego łatwo wyliczysz
promień tego większego R spełnia równanie
√2*R=R+4+√2*4
są dwa takie koła
tu na rysunku to o mniejszym promieniu r
|SO|=√2*4
|SO|=4+r+√2*r
czyli √2*4=4+r+√2*r i z tego łatwo wyliczysz
promień tego większego R spełnia równanie
√2*R=R+4+√2*4
 a tu widać to drugie większe koło i to małe
a tu widać to drugie większe koło i to małe
 zacznijmy od tego, że środek tego okręgu leży na prostej y = x lub y = −x
mały niebieski trójkąt to trójkąt równoramienny o podstawie = 4−r i ramionach równych
(oczywiście r>0 i r<4)
z tw. Pitagorasa:
r2 + r2 = (4−r)2
2r2 = 16 − 8r + r2
r2 + 8r − 16 = 0
Δ = 2*64
zacznijmy od tego, że środek tego okręgu leży na prostej y = x lub y = −x
mały niebieski trójkąt to trójkąt równoramienny o podstawie = 4−r i ramionach równych
(oczywiście r>0 i r<4)
z tw. Pitagorasa:
r2 + r2 = (4−r)2
2r2 = 16 − 8r + r2
r2 + 8r − 16 = 0
Δ = 2*64
 no właśnie, nie narysowałam okręgu x2+y2≤16
no właśnie, nie narysowałam okręgu x2+y2≤16


 ale że nie odpuszczam kół stycznych zewnętrznie, to może jeszcze takie cztery koła o promieniu
R spełnią warunki zadania?
√2*R=4+R
ale że nie odpuszczam kół stycznych zewnętrznie, to może jeszcze takie cztery koła o promieniu
R spełnią warunki zadania?
√2*R=4+R
