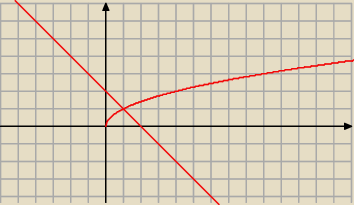
Całka podwójna - drobna podpowiedź Xwd: Witam, czy mógłbym prosić któregoś z tutejszych matematyków o potwierdzenie mojego rozumowania? Mam do policzenia całkę podwójną: ∬xydxdy po obszarze ograniczonym D, ograniczony jest powierzchniami: y=0, y=√x, x+y=2 Liczę więc całkę według osi OX: D={(x,y)∊R² : 0≤x≤1 , √x≤y≤2−x} Dobrze zdefiniowałem obszar całkowania?

Adamm: nie najlepiej wyznaczyć obszar względem y D={(x, y)∊R²: 0≤y≤1, y²≤x≤2−y}

Xwd: Dlaczego?

Adamm: gdyby obszar był wyznaczony przez krzywe x=0, x+y=2, y=√x to byłoby w porządku (ten obszar zaznaczyłeś) ale tak nie jest

Xwd: No tak, mój błąd.... Zaznaczyłem na swoim rysunku x=0. No nic, dzięki wielkie za pomoc