Równanie prostej Alucarddo: Wyznacz równanie prostej przechodzącej przez punkt (√3,−2) a) prostopadłej do prostej 3√6 −6y −4 = 0 b) nachylonej do osi OX pod kątem 120° Proszę o dokładne, łopatologiczne wytłumaczenie bo to dla mnie czarna magia.

Alucarddo: 3√6x*

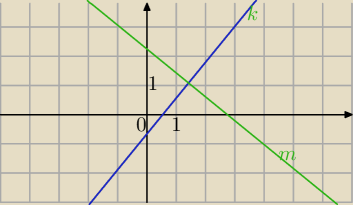
Mila: a) k: 3√6x−6y−4=0 m⊥k i A=(√3,2)∊m wektory: [3√6,−6]⊥[6,3√6] m: 6x+3√6y+C=0 6*√3+3√6*(−2)+C=0 6√3−6√6+C=0 C=6√6−6√3 m: 6x+3√6y+6√6−6√3=0 /:3 m: 2x+√6y+2√6−2√3=0

Alucarddo: Punkt A to (√3, −2) więc chyba nie tak

Alucarddo: rozwiązanie zadania to : y = −√6/3x + √2 − 2 za Chiny nie wiem jak to zrobić

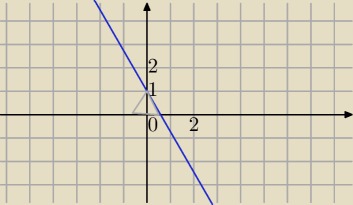
Mila: Wyznacz równanie prostej przechodzącej przez punkt (√3,−2) b) nachylonej do osi OX pod kątem 120° m: y=ax+b a=tg(120^o)=tg(180−60)=−tg(60)=−√3 y=−√3x+b i A=(√3,−2)∊m⇔ −2=−√3*√3+b b=1 m: y=−√3x+1 ==========

Mila: Podstawiłam dobry punkt i masz równanie ogólne, można go przekształcić. ( ale nie musisz, to jest dobre równanie) 2x+√6y+2√6−2√3=0 √6*y=−2x−2√6+2√3 /:√6

	−2		2√3
y=		x−2+
	√6		√6

	−2√6		2
y=		x−2+
	6		√2

	−√6
y=		*x−2+√2
	3

================

Alucarddo: Dobrze, a dlaczego to 6x+3√6y+C=0 nie wygląda tak " −6x −3√6y +c =0?

Alucarddo: O boże, już to rozwiązałem kilka razy szczerze mówiąc, kilka razy wyliczyłem C dokładnie tak samo, ale nie wiedziałem że tyle wystarczy :v

Alucarddo: Ale dalej nie wiem dlaczego nie jest to −6x −3√6

Mila: Też może być. 1) Jeżeli masz prostą podaną równaniem ogólnym Ax+By+C=0 to prostopadła do niej ma równanie: Bx−Ay+D=0 albo −Bx+Ay+D=0 Przykład: k: 2x+5y+2=0 m: 5x−2y+D=0 bo iloczyn skalarny wektorów [2,5] i [5,−2] jest równy 0 2*5+5*(−2)=0⇔wektory są prostopadłe m⊥k 2) Jeżeli masz prostą podaną równaniem kierunkowym: k: y=2x+4

	1
m: y=−		x+b
	2

m⊥k a₁*a₂=−1 warunek prostopadłości

	1
2*(−		)=−1
	2

Jeżeli masz jeszcze pytania, to pisz , po kolacji odpowiem

Alucarddo: Jesteś moim wybawcą tak szczerze mówiąc, bo ja z rozszerzenia cienki bolek jestem ale teraz przynajmniej to zadanie rozumiem, i co źle zrobiłem. Wielkie dzięki

Mila: No to trzeba się zacząć porządnie uczyć