Relacje... kleszcz: 2. X − zbiór wszystkich prostych na płaszczyźnie; a) k R l ⇔ proste te są do siebie równoległe; Moim zdaniem wynikającym czysto z domysłów xD a) przeciwzwrotna... b) k R l ⇔ proste te mają dokładnie jeden punkt wspólny; b) symetryczna, przechodnia... c) k R l ⇔ proste te mają co najmniej jeden punkt wspólny; c) symetryczna, przechodnia... No niestety nie jestem w tym dobry

Blee: a) na pewno synetryczna (skoro k rownolegla do l to l rownolegla do k) i przechodnia b) nie jest przechodnia. Niech k : y=x ; l : y =−x ; m: y= x+1 k i m sa rownolegle wiec nie sa w relacji c) to samo

kleszcz: Dzięki

kleszcz: Aha jeszcze zapomniałem dodać polecenie jest takie jak wcześniej do tego zadania: "W poniższych zadaniach zbadaj, które z siedmiu znanych własności(zwrotna, przeciwzwrotna, symetryczna, przeciwsymetryczna, antysymetryczna, przechodnia, spójna) posiada każda relacja R ⊂ X x X. Ponadto określ, która z relacji jest relacją porządku, a która relacją równoważności. W przypadku relacji równoważności opisz jej klasy abstrakcji."

iteRacj@: a) k R l ⇔ proste te są do siebie równoległe zwrotna, symetryczna, przechodnia czyli jest to relacja równoważności spróbuj określić jej klasy abstrakcji, inaczej się tego nie nauczysz a dlaczego uważasz, że jest przeciwzwrotna?

kleszcz: Po prostu wydawało mi się że skoro proste nie przecinają się to nie są w relacji same ze sobą, czyli przeciwzwrotne

iteRacj@: Trzeba zadać pytanie, czy prosta dowolna prosta na płaszczyźnie jest równoległa do siebie samej? Dwie proste na płaszczyźnie są równoległe, jeżeli nie przecinają się w żadnym punkcie lub mają nieskończenie wiele puniktów wspólnych (pokrywają się). A stąd wynika, że każda prosta jest do siebie samej równoległa. Czyli relacja z punktu a) jest zwrotna. Spróbuj określić czy zwrotne lub przeciwzwrotne są relacje z pkt b) i c)

kleszcz: OK już troszkę rozjaśniło przynajmniej a) zwrotna, symetryczna, przechodnia > równoważności Klasy Abstrakcji [proste równoległe]R = {prosta A, prosta B}

kleszcz: [wszystkie proste równoległe na płaszczyźnie]

kleszcz: bardziej {prosta A, prosta B... prosta n} − w sumie nie wiem

kleszcz: W takim razie jak proste mają ten jeden punkt wspólny to są już zwrotne tak?

kleszcz: Czy przeciwzwrotna bo pozostałe punkty się nie pokrywają?

kleszcz: w b) przeciwzwrotna, antysymetryczna, przeciwsymetrycza (?)

ite: a) k R l ⇔ proste te są do siebie równoległe Kierunek − to zbiór wszystkich prostych równoległych do danej prostej, takie zbiory to są właśnie klasy abstrakcji w tej relacji. Jest ich nieskończenie wiele.

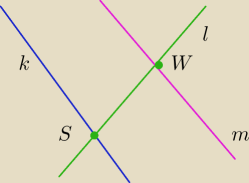
ite: b) k R l ⇔ proste te mają dokładnie jeden punkt wspólny Prosta k ma nieskończenie wiele punktów wspólnych z samą sobą, warunek dokładnie jednego pkt wspólnego nie jest spełniony. Więc ¬kRk, nie jest prawdą, że prosta k pozostaje w relacji R sama ze sobą. Relacja nie jest zwrotna. Ponieważ żadna inna prosta też nie pozostaje w relacji R sama ze sobą, to żadna para pRp nie należy do relacji. Relacja jest przeciwzwrotna. Tak jak napisał Blee ta relacja nie jest przechodnia. Proste k i l mają dokładnie jeden pkt wspólny S, proste m i l też mają dokładnie jeden pkt wspólny W, ale proste k i l już nie mają żadnego pkt wspólnego. Jeśli istnieje chociaż jedna para, która tego warunku nie spełnia, to relacja nie może być przechodnia, tutaj istnieją takie pary. Oczywiście jest symetryczna. Dlaczego? I z tego wynika, że nie jest ani antysymetryczna, ani przeciwsymetryczna. Nie jest spójna. Dlaczego?