obszar popek: Potrzebuje przedział obszaru całkowania gdzie D jest obszarem ograniczonym krzywymi y=x²−3, y+1=x Pewnie tam trzeba to jakoś podzielić, ale nie mam pojęcia jak. Ktos pomoże?

popek: Fajnie gdyby był rysunek. Dziękuje.

jc: Przecięcie prostej z parabolą: x−1=x²−3 x²−x−2=0 x=−1 lub x=2 Obszar: −1 ≤ x ≤ 2 x²−3 ≤ y ≤ x−1 (prosta i parabola rozcinają płaszczyznę na 5 części, z których tylko opisana powyżej jest ograniczona).

popek: Ograniczony, czyli jest raz z góry i raz z dołu, prawda? Ale nie umiem sobie tego zobrazować. Dlaczego na 5?

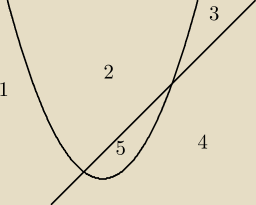
jc: Tyko piąty fragment jest ograniczony. Pozostałe fragmenty rozciągają się dowolnie daleko.

popek: A tak, to ja myslalem wlasnie tylko o tym 5. To równanie liniowe miało być x+y=1, ale zamysł ogolnie ten sam. Czyli będzie x−1≤y≤x²−3?

jc: Nie. Będzie tak: 1−x ≤ y ≤ x²−3

popek: znów pomyliłem Dzieki

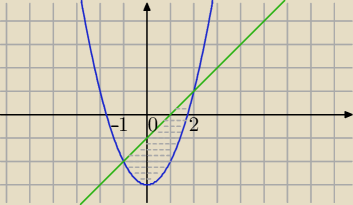
Mila: y=x²−3, y+1=x y=x−1 x²−3=x−1 x²−x−2=0⇔x=−1 lub x=2 ∫₋₁²∫_x²−3^x−1 f(x,y) dy dx