Nierówność kwadratowa z wartością bezwzględną Pochodny: Mam problem z rozwiązaniem zadania. |(x²−5x+3)/(x²−1)|<1. Proszę o pomoc

piotr:

x2−5x+3		x2−5x+3
	> −1 ∧		< 1
x2−1		x2−1

(x−2) (x−1/2)		x−4/5
	> 0 ∧		> 0
(x−1) (x+1)		(x−1) (x+1)

Lech: Koniecna jest dziedzina : x= R − { −1 , 1}

Pochodny: Ok. A wie ktoś jak to będzie wyglądało na wykresie

PW: Mam dwa pytania: − Dlaczego nazywasz to nierównościa kwadratową? − Co to znaczy "Jak to będzie wyglądało na wykresie"?

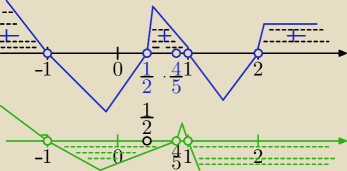
Mila: |(x²−5x+3)/(x²−1)|<1 x≠1 i x≠−1

	x2−5x+3
−1<		<1
	(x2−1)

	x2−5x+3		x2−5x+3
−1<		i		<1
	(x2−1)		(x2−1)

x2−5x+3		x2−5x+3
	+1>0 i		−1<0
(x2−1)		(x2−1)

x2−5x+3+x2−1		x2−5x+3−x2+1
	>0 i		<0
(x2−1)		x2−1

(2x²−5x+2)*(x−1)*(x+1)>0 i (−5x+4)*(x−1)*(x+1)<0⇔

	1		4
2*(x−		)*(x−2)*(x−1)*(x+1)>0 i 5*(−x+		)*(x−1)*(x+1)<0
	2		5

	1		4
x∊(−∞,−1)∪(		,1)∪(2,∞) i x∊(−1,		)∪(1,∞)⇔
	2		5

	1		4
x∊(		,		)∪(2,∞)
	2		5

========================