geometria analit.
asia: cześć, zrobi ktoś? ja nie ogarniam
dane są punkty A=(−1,−5), B(−2,1). Punkty P i R dzielą ten odcinek na trzy równe części.
Wyznacz współrzędne punktów P i R.
jeżeli da radę to bez użycia wektorów poproszę + jakiś rysunek jeśli da radę

z góry dzięki!
17 maj 22:42
Nie da rady:
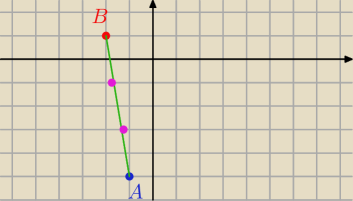
masz odcinek A−>B
tak ciezko go podzielic na 3 czesci?
a jak bys miala odcinek dlugosci 6
to jak go podzielic na 3 rowne czesci?
normalnie bez komentarza.
co sie dzieje z tym dzisiejszym pokoleniem...
17 maj 23:05
asia: tyle to też umiem łbie xd
17 maj 23:08
asia: dzięki za pomoc xd
17 maj 23:08
Nie da rady:
A(−1,−5),
B(−2,1)
odleglosc pomiedzy −1 , −2 to 1 (iksy)
odleglosc pomiedzy −5 , 1 to 6 (igreki)
zatem jak dzielisz na 3 odcinki to mamy
1/3 dla iksow, 6/3 = 2 dla igrekow
stad
Patrzymy co musimy zrobic zeby znajdowac sie w odcinku
do punktu A dodajemy 1/3 do iksa czy odejmujemy?
oczywiscie odejmujemy, bo odcinek <−1; −2>
zatem nowe punkty pomiedzy A i B maja iksy:
−1 − 1/3 = −4/3 oraz −1 −1/3 − 1/3 = −4/3 − 1/3 = −5/3
no to igreki
zeby miec od −5 do 1 trzeba dodac 2 czy odjac
oczywiscie trzeba dodac, zatem te punkty z powyzej co maja juz iksy, no to ich igreki:
−5+2 = −3 , −5+2+2 = −3+2 = −1
zatem punkty w srodku:
(−4/3, −3)
(−5/3, −1)
17 maj 23:22
Nie da rady:
to moze rozwiazanie z wektorem:
co to jest wektor?
wektor to jest przesuniecie.
spojrzmy na to w ten sposob
jestesmy w punkcie A(−1,−5)
co musimy zrobic aby dostac sie do punktu B(−2,1)
musimy cos odjac/dodac do iksa, oraz cos odjac/dodac do igreka
(w sensie wspolrzednych iksowych i igrekowych punktu A)
zeby od −1 cos dodac i w efekcie byc w −2 to te cos wynosi −1
zeby od −5 cos dodac i w efekcie byc w 1 to te cos wynosi 6
zatem nasz wektor AB = [−1,6]
tym razem zeby to policzyc to zgadywalismy.
Mozna jednak zauwazyc , ze wystarczy odjac wspolrzedne punktu koncowego
od wspolrzednych punktu poczatkowego...
ze tak brzydko napisze B − A
i wtedy mamy wektor AB = [−2 −(−1), 1 − (−5)] = [−2+1, 1+5] = [−1, 6]
Skoro wektor mowi ze o przesunieciu
to jak do punktu A dodam wektor AB to jestem w punkcie B
ale skoro chcemy podzielic ten caly odcinek na 3 mniejsze
to wystarczy podzielic wektor AB / 3 czyli kazda wspolrzedna tego wektora
zatem 1/3AB = [−1/3 , 6/3] = [−1/3, 2]
i teraz do punktu A dodaje ten wektor 1/3AB
a potem do wynikowego punktu znowu dodaje 1/3AB
zatem
1) do A(−1,−5) dodaje wektor [−1/3, 2]
i otrzymuje punkt (−1−1/3, −5+2) = (−4/3, −3)
2) teraz do punktu (−4/3 , −3) dodaje znowu wektor [−1/3, 2]
i mam punkt (−5/3, −1)
wyszlo nam to samo co 23:22
a jednak to jest szybsze i trzeba mniej myslec.
Prosze sie nie bac wektorow, one nie gryza, co najwyzej przesuwaja sie
jak to wektory

17 maj 23:35
Eta:
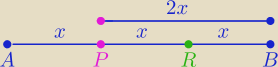
Podział odcinka AB punktem P w stosunku k=2
| | k*xA+xB | | k*yA+yB | |
ze wzoru : xP= |
| i yP= |
| |
| | k+1 | | k+1 | |
| | −2−2 | | −4 | | −10+1 | |
to xP= |
| = |
| i yP= |
| = −3 |
| | 3 | | 3 | | 3 | |
P(−4/3, −3)
========
R jest środkiem odcinka PB
| | xP+xB | | | | −4−6 | | 5 | |
to xR= |
| = |
| = |
| = − |
| |
| | 2 | | 2 | | 6 | | 3 | |
| | yP+yB | |
yR= |
| = ...............= −1 |
| | 2 | |
==========
18 maj 00:00
 z góry dzięki!
z góry dzięki!
 masz odcinek A−>B
tak ciezko go podzielic na 3 czesci?
a jak bys miala odcinek dlugosci 6
to jak go podzielic na 3 rowne czesci?
normalnie bez komentarza.
co sie dzieje z tym dzisiejszym pokoleniem...
masz odcinek A−>B
tak ciezko go podzielic na 3 czesci?
a jak bys miala odcinek dlugosci 6
to jak go podzielic na 3 rowne czesci?
normalnie bez komentarza.
co sie dzieje z tym dzisiejszym pokoleniem...

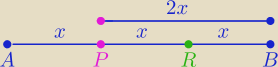 Podział odcinka AB punktem P w stosunku k=2
Podział odcinka AB punktem P w stosunku k=2