czworokąt x&y&z: Dany jest czworokąt wypukły ABCD . Przekątna BD dzieli ten czworokąt na dwa trójkąty o równych polach Punkty E i F są odpowiednio środkami boków AD i BC Odcinek EF przecina przekątną BD w punkcie M Wykaż że |EM|=|MF|

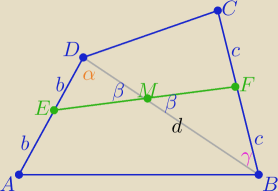
Eta: 1/ rysunek |AD|=2b, |BC|=2c , |BD|=d

	1		1
P(ABD)=		*2b*d*sinα i P(BCD)=		*2c*d*sinγ
	2		2

z treści zadania z równości pól otrzymujemy:

	bsinα
bsinα=csinγ ⇒ c=
	sinγ

2/ z tw. sinusów w ΔEDM i w ΔBFM

|EM|		b		|MF|		c
	=		i		=
sinα		sinβ		sinγ		sinβ

	bsinα		csinγ		bsinα		sinγ		bsinα
|EM|=		i |MF|=		=		*		=
	sinβ		sinβ		sinγ		sinβ		sinβ

zatem : |EM|=|MF| c.n.w

anaisy: A₁, E₁, F₁, C₁ są rzutami A, E, F, C na BD odpowiednio. Z tw. Talesa

	DE		EE1
2=		=		, czyli EE1=12AA1.
	DA		AA1

Analogicznie FF₁=¹₂CC₁. Gdy EM prostopadłe do DB, to M=E₁=F₁, czyli koniec. Załóżmy więc, że nie. Skoro pola ADB i DBC są równe to AA₁=CC₁, więc EE₁=FF₁. Mamy ∡EE₁M=∡MF₁F, ∡EME₁=∡F₁MF, czyli też ∡E₁EM=F₁FM, stąd z kbk trójkąty EE₁M i FMF₁ są przystające czyli EM=MF