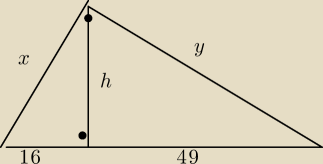
 rysunek do pierwszego zadania jak obliczyć h,x,y i pole nie wiem jak obliczyc h z reszta sobie
poradzę
dzięki
rysunek do pierwszego zadania jak obliczyć h,x,y i pole nie wiem jak obliczyc h z reszta sobie
poradzę
dzięki
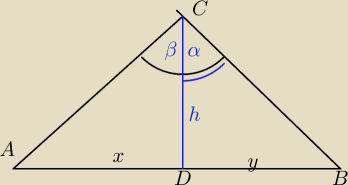 Raczej z podobienstwa trojkatow
α+β=90o
AD=x−−−rzut przyprostokatnej AD na przeciwrostokatna AB
DB=y −−−rzut przyprostokatnej BC na przeciwprostokatna AB
x+y=AB − dlugosc przeciwprostokatnej
Sredna geometryczna (a) dwoch liczb (bi c ) jest rowna pierwiastkowi kwadratowego z iloczynu
tych liczb
a= √b*c to juz wiadomo w klasie 7
Tw. W trojkacie prostokatnym wysokosc wykreslona z wierzchoklka kata prostego na
przeciwprostokatna jest srednia geometryczna
obu odcinkow na jakie podzielila przeciwprostokatna
Zalozenie
∡C=90o i h⊥AB
Teza AD : h = h ; DB
Dowod ; Rozpatrujemy trojkaty ACD i DBC
Sa podobne na podstawie pierwszej cechy podobienstwa trojkatow bo
∡ACD=∡CDB jako proste
∡β= ∡B jkao katy o ramionack parami prostopadlych (AC⊥CB i CD⊥AB )
Z podobienstwa tych trojkatow wynika proporcjonalnosc odpowiednich bokow
AD : h = h : DB
x : h = h : y
Raczej z podobienstwa trojkatow
α+β=90o
AD=x−−−rzut przyprostokatnej AD na przeciwrostokatna AB
DB=y −−−rzut przyprostokatnej BC na przeciwprostokatna AB
x+y=AB − dlugosc przeciwprostokatnej
Sredna geometryczna (a) dwoch liczb (bi c ) jest rowna pierwiastkowi kwadratowego z iloczynu
tych liczb
a= √b*c to juz wiadomo w klasie 7
Tw. W trojkacie prostokatnym wysokosc wykreslona z wierzchoklka kata prostego na
przeciwprostokatna jest srednia geometryczna
obu odcinkow na jakie podzielila przeciwprostokatna
Zalozenie
∡C=90o i h⊥AB
Teza AD : h = h ; DB
Dowod ; Rozpatrujemy trojkaty ACD i DBC
Sa podobne na podstawie pierwszej cechy podobienstwa trojkatow bo
∡ACD=∡CDB jako proste
∡β= ∡B jkao katy o ramionack parami prostopadlych (AC⊥CB i CD⊥AB )
Z podobienstwa tych trojkatow wynika proporcjonalnosc odpowiednich bokow
AD : h = h : DB
x : h = h : y
| x | h | ||
= | ⇒ h2=x*y ⇒h=√x*y cnd | ||
| h | y |

 "blee" .......małą literą ! "Pitagoras"........ wielką literą !
"blee" .......małą literą ! "Pitagoras"........ wielką literą !
 h=28
Mozesz z tw Pitagorasa albo skorzystac z nastepnego twierdzenia dotyczacego trojkata
prostokatnego
Twierdzenie
W trojkacie prostokatnym przyprostokatna jest srednia geometryczna przeciwprostokatnej i swego
rzutu na przeciwprostokatna
czyli AC= √AB*AD=√65*16=√16*√65= 4√65
BC=√ab*DB= √65*49=√49*√65= 7√65
h=28
Mozesz z tw Pitagorasa albo skorzystac z nastepnego twierdzenia dotyczacego trojkata
prostokatnego
Twierdzenie
W trojkacie prostokatnym przyprostokatna jest srednia geometryczna przeciwprostokatnej i swego
rzutu na przeciwprostokatna
czyli AC= √AB*AD=√65*16=√16*√65= 4√65
BC=√ab*DB= √65*49=√49*√65= 7√65
 Wczoraj pozno w nocy wrocilem do domu . Bylem u corki 2 tygodnie odpoczalem . Juz po
niedzieli do pracy
Wczoraj pozno w nocy wrocilem do domu . Bylem u corki 2 tygodnie odpoczalem . Juz po
niedzieli do pracy


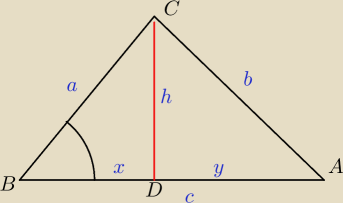

 UWAGA
============
Musisz zwracac uwage na to aby w zapisie symboliczym przystawania i podobienstwa trojkakow
wierzcholki trojkatow wymieniac w kolejnosci zgodnej z ich wzajemna odpowiedniscia
Czyli jesli wierzcholki jednego trojkata wymieniamy np w kolejnosci od najmniejszego kata do
najwiekszego to wdrugim trojkacie
nalezy wymieniac w takiej samej kolejnosci
Zeby sie nie przyzwyczajac do oznaczen zmienilem je
Wiec teraz ta kolejnosc bo w trojkatach podobnych boki sa proprcjonalne
ΔABC∼ΔCBD∼ΔACD
AB : BC=CB : BD= AC : CD
inaczej
c : a=a : x= b : h *(1)
Bierzemy czesc proporcji * (1) czyli c : a= a : x ⇒a2= c*x⇒a= √c*x
Zamieniamy przyprostokatne a i b i ich rzuty x i y otrzymamy z *(1) rownosc
c : b= b : y= a : h ⇒b2= c*y⇒b= p[c*y}
Teraz samemu ze h= √x*y
UWAGA
============
Musisz zwracac uwage na to aby w zapisie symboliczym przystawania i podobienstwa trojkakow
wierzcholki trojkatow wymieniac w kolejnosci zgodnej z ich wzajemna odpowiedniscia
Czyli jesli wierzcholki jednego trojkata wymieniamy np w kolejnosci od najmniejszego kata do
najwiekszego to wdrugim trojkacie
nalezy wymieniac w takiej samej kolejnosci
Zeby sie nie przyzwyczajac do oznaczen zmienilem je
Wiec teraz ta kolejnosc bo w trojkatach podobnych boki sa proprcjonalne
ΔABC∼ΔCBD∼ΔACD
AB : BC=CB : BD= AC : CD
inaczej
c : a=a : x= b : h *(1)
Bierzemy czesc proporcji * (1) czyli c : a= a : x ⇒a2= c*x⇒a= √c*x
Zamieniamy przyprostokatne a i b i ich rzuty x i y otrzymamy z *(1) rownosc
c : b= b : y= a : h ⇒b2= c*y⇒b= p[c*y}
Teraz samemu ze h= √x*y
