Nierówność z wartością bezwzględną Axsiu: Cześć. Mam kłopoty z zadaniem |(5x−3)/(2x+7)|<2

Jerzy:

	5x − 3
−2 <		< 2
	2x + 7

Axsiu: Ja to robię w ten sposób, że sprowadzam 2 do lewej strony i mam (x−17)/(2x−7)<0. Teraz określam warunki spełnienia nierówności tj. 1.licznik dodatni i mianownik ujemny lub 2. na odwrót; to samo z (5x−3)/(2x+7)>−2. Problem w tym, że z pierwszej nierówności wychodzi mi z 1. x<17 lub x>7/2 a z 2. x>17 lub x<7/2 i nie wiem co robić z tym.

Axsiu: Jerzy to już wiem

Jerzy:

5x − 3		2(2x + 7)		5x − 3 − 4x − 7
	−		< 0 ⇔		< 0
2x + 7		2x + 7		2x + 7

	x − 10		7
⇔		< 0 ⇔ (x −10)(2x + 7) < 0 ⇔ x ∊ (−		;10)
	2x + 7		2

Jerzy: To była nierówność: U < 2 Teraz druga nierówność: − 2 < U

Jerzy:

	x − 17		7
Upss .. pomyłka.		} < 0 ⇔ (x − 17)(2x + 7) < 0 ⇔ x ∊ (−		;17)
	2x + 7		2

Jerzy:

	7		11
Z drugiej nierówności dostaniesz: x ∊ ( − ∞;−		) U (−		;+∞)
	2		9

i teraz część wspólna obydwu rozwiazań.

Axsiu: Dzięki wielkie. Nie zauważyłem, że da się to zrobić tak szybko a Krysicki z Włodarskim mi tak na około tłumaczyli. Jeszcze raz dziękuje

Axsiu: A wiesz jak zrobić to |(2x−5)/(x+3)|>1. Robiąc tą metodą wyszło mi x∊(−∞,−3)∪(8,+∞) a z drugiego x∊(−3, 2/3). Nie widzę tu żadnej części wspólnej a w odpowiedziach piszę x<−3 lub −3<x<2/3 lub x>8

Jerzy: Pokaż obliczenia , znajdziemy błąd.

Jerzy: Masz dobrze, tylko w tym przypadku nie szukasz części wspólnej, tylko sumy rozwiazań.

Jerzy: |U| > 1 ⇔ U > 1 lub U < −1

Axsiu: (2x−5)/(x+3)>1 (x−8)/(x+3)>0 x∊(−∞,−3)∪(8,∞) (2x−5)/(x+3)<−1 (3x−2)/(x+3)<0 (3x−2)(x+3)<0 x∊(−3,2/3)

Axsiu: Od czego zależy czy szukam iloczynu czy sumu?

Jerzy: |x| ≤ A ⇔ − A ≤ x ≤ a |x| ≥ A ⇔ x ≥ A lub x ≤ − A

Axsiu: OK. Jeszcze jedna rzecz, wiesz jak zrobić tego typu nierówność z ułamkiem lecz z pierwiastkiem kwadratowym zamiast wart. bez.?

Jerzy: Nie rozumiem pytania. Podaj konkretny przykład.

Axsiu: √(3x−1)/(2−x)>1

Axsiu: podnieść do kwadratu całą nierówność?

Jerzy: 1) założenie: (3x − 1)(2 − x) ≥ 0 2) obustronnie do kwadratu

Axsiu: (3x−1)/(2−x)>1 (4x−3)/(2−x)>0 x∊(−∞,3/4) ∩(2,+∞) Lecz w odpowiedziach jest x∊(3/4,2)

Jerzy: Sorry nie zauważyłem,że pod pierwiastkiem jest ułamek, czyli inne załozenia: 1) 2 − x ≠ 0

	3x − 1
2)		⇔ (3x − 1)(2 − x) ≥ 0
	2 − x

PW: (4x−3)(2−x)>0 ⇔(4x−3)(x−2)<0 [przemnożenie obnu stron przez −1 bardzo pomaga to zobaczyć]

	3
⇔ x∊(		,2)
	4

Jerzy: (4x − 3)(2 − x) > 0 ⇔ x ∊ (3/4;2) ... przecież gałęzie paraboli są skierowane w dół.

Axsiu: A to nie jest tak, że w nierowności liniowej decyduje znak nierówności?

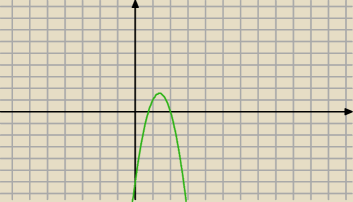
Jerzy: Przecież po lewej stronie masz funkcję kwadratową: (4x − 3)(2 − x) i jej wykres

Jerzy: Widzisz w jakim przedziale lewa strona jest dodatnia ?

Axsiu: Wszystko już rozumiem. Dzięki bardzo