wyznaczenie równania Piotr: Cześć ma takie zadanko mam trapez równoramienny o podstawach 2 3 oraz ramionach o długości 1,5 i prostą m odległą o 0,5 od krótszej podstawy trapezu od trapezu równoległą do podstaw. Moje L zależy od długości po długości podstawy trapezu(zmienia się od 2 do 3), oś x jest prostopadła do prostej m. muszę wyznaczyć L w zależności od x. Wynik to 2x+1

Jerzy: To bełkot.

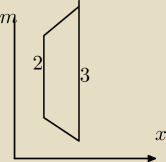
Piotr: długość l zmienia się od 2 do 3 odległość prostej m od boku 2 wynosi 0,5 ramię trapezu wynosi 1,5 Mam wyznaczyć l od x

Jerzy: A co to jest l ? Co to znaczy: " długość l zmienia się od 2 do 3 "

Piotr: w miare postępowania x długość zmienia się od boku trapezu od 2 do 3

Jerzy: Co to jest l ?

Boniek: L to jest odległość między ramionami dla kolejnych x

Blee: 1) wyznaczamy a z tw. pitagorasa

	9		5		√5
a2 =		− 1 =		−> a =
	4		4		2

2) nie wiemy jak daleko 'oddalony' jest trapez od osi OY 3) załóżmy, że 'odległość' krótszej podstawy od osi OY wynosi b = 5, wtedy:

	(x−5)		2√5(x−5)
L(x) =		+ 2 =		+ 2
	a		5

Blee: oczywiście, źle wyznaczone 'a'

	9		1
a2 =		−		= 2 −> a = √2
	4		4

	√2(x−b)
więc L(x) =		+ 2 ; gdzie b = 'odległość' krótszej podstawy od osi OY
	2

Jerzy:

	1
b =
	2

Blee: Jerzy ... Ty się tego domyślasz, wiesz że prosta 'm' jest w odległości 0.5 od krótszej podstawy. Nie wiesz jednak czy jest ona na osi OY czy też nie. Zapewne tak, ale po tym co napisał autor − nie ma co do tego pewności.

Jerzy: Racja