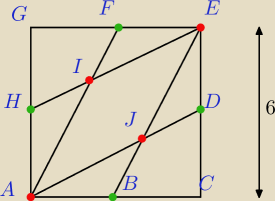
 Proszę spojrzeć na rysunek. Przedstawia on kwadrat ACEG o boku 6. Punkty B, D, F, H są środkami
poszczególnych boków. Połączono je z poszczególnymi wierzchołkami, tak jak na rysunku obok.
Zadanie polega na obliczeniu pola rombu AJEI.
I teraz tak, udało mi się obliczyć to metodami wyznaczenia sinusa kąta, potem przekątna,
korzystając
z tw. cosinusów obliczyłem że pole wynosi 12 i to jest pewne, jednak problem polega na czym
innym:
chodzi o to, by to zadanie rozwiązać bez korzystania z funkcji trygnometrycznych, na poziomie
gimnazjum. To że pole wynosi 12 jest oczywiste, ale jak do tego dojsc nie znając sin, cos?
Proszę spojrzeć na rysunek. Przedstawia on kwadrat ACEG o boku 6. Punkty B, D, F, H są środkami
poszczególnych boków. Połączono je z poszczególnymi wierzchołkami, tak jak na rysunku obok.
Zadanie polega na obliczeniu pola rombu AJEI.
I teraz tak, udało mi się obliczyć to metodami wyznaczenia sinusa kąta, potem przekątna,
korzystając
z tw. cosinusów obliczyłem że pole wynosi 12 i to jest pewne, jednak problem polega na czym
innym:
chodzi o to, by to zadanie rozwiązać bez korzystania z funkcji trygnometrycznych, na poziomie
gimnazjum. To że pole wynosi 12 jest oczywiste, ale jak do tego dojsc nie znając sin, cos?
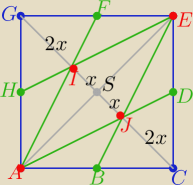 |AE|=6√2 , |CG|=6√2= 6x ⇒ 2x=2√2=|CG|
|AE|=6√2 , |CG|=6√2= 6x ⇒ 2x=2√2=|CG|
| 1 | ||
P(AJEI)= | *|AE|*|IJ| = 3√2*2√2=12 | |
| 2 |
| 1 | ||
|GI|=|IJ|=|JC|= | |GC| | |
| 3 |
| 6√2 | 6√2 | 1 | ||||
P= | * | * | 3√2 | |||
| 2 | 2 | 6√2−3√2/2 |