1 LO zadanie z geometrii Sandra: Udowodnij że każdy z dwóch odcinków, na które dwusieczna kąta wewnętrznego dzieli przeciwległy bok jest krótszy od tego boku trójkąta, z którym ma wspólny koniec

Sandra: Dowód ma być na symbolach

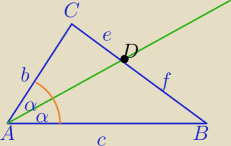
Mila: Z. AD^→dwusieczna kata A w ΔABC T. e<b i f<c 1) Z tw. o dwusiecznej kąta wewnętrznego w trójkącie:

b		c
	=		i e+f=a⇔
e		f

b*f=e*c i e=a−f b*f=(a−f)*c⇔b*f=a*c−f*c b*f+f*c=a*c f*(b+c)=a*c

	a*c		a*c
2) f=		i b+c>a⇔f<		=c ( zmniejszono mianownik ułamka , a>0,b>0 ,c>0)
	b+c		a

⇔f<c

	a*b		a*b
3) e=		i b+c>a⇔e<		=b⇔
	b+c		a

e<b =====================================

Mila:

Sandra: Wielkie dzięki

Blee: Można było także inaczej: Nie wprost (posiłkujemy się wcześniejszym wykresem) Niech b<e 1) Z tw. o dwusiecznych:

b		c
	=		⇒ c < f (tutaj sprzeczność mamy przy założeniu b<e i c>f)
e		f

czyli b+c < e+f = a <−−− niespełniona nierówność trójkąta sprzeczność

Sandra: Mila, mogłabyś mi wytłumaczyć skąd wyznaczyłaś, że e=a*b/b+c?

Mila:

	a*c		a*(b+c)−a*c
e=a−f=a−		=		=
	b+c		b+c

	a*b+ac−ac		a*b
=		=
	b+c		b+c

Sandra: Dziękuję bardzo 😊

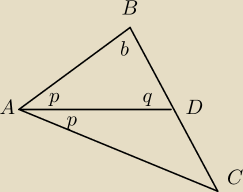
jc: p, b, q = kąty AB ≤ BD ⇒ p ≥ q 180 = p+q+b ≥ 2p + b (sprzeczność, 2 kąty trójkąta A, B,C muszą mieć mniej niż 180). Przy okazji, dziękuję Milu za zapoznanie mnie z nowym twierdzeniem