Pochodna funkcji 793255: Czemu funkcja f(x)=lxl jest ciągła ale nie jest różniczkowalna ?

Adamm: Jest ciągła z przyczyn oczywistych a nie jest różniczkowalna, bo pochodna w zerze nie istnieje

Lech : Poniewaz dla x≥ 0 , f(x) = x , f '(x) = 1 dla x< 0 , f(x) = −x , f '(x) = −1

Adamm: Jeśli chcemy być bardziej szczegółowi, to f'(x)=1 dla x>0

Lech : Tak Adamm masz racje ,blad w druku !

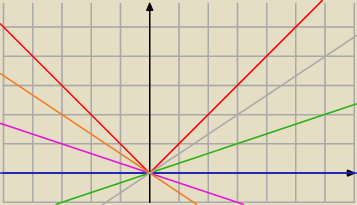
Blee: albo jak wolisz 'ilustracyjnie': Interpretacja geometryczna wartości pochodnej (w punkcie) to tanges kąta nachylenia stycznej wykresu tejże funkcji w tymże punkcie. Teraz narysujmy f(x) = |x| i jak łatwo zauważyć, dla x=0 mamy nieskończenie wiele stycznych do tegoż wykresu. Dlatego właśnie, funkcja f(x) = |x| nie jest różniczkowalna w całej swojej dziedzinie.