Geometria Lolek: Dany jest czworokąt abcd. Punkty K i L są odpowiednio środkami boków bc i cd. udowodnij że suma pół trójkątów abk i adl jest większa od pola trójkąta AKL

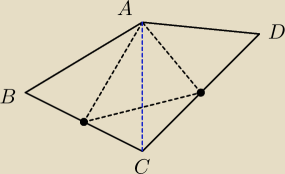
Blee: Jako, że punkt K jest środkiem BC to: P_ΔABK = P_ΔAKC (ta sama podstawa i ta sama wysokość) <−−− odpowiednie tw. o środkowej analogicznie P_ΔADL = P_ΔADC Zatem: P_ΔABK + P_ΔADL = P_ΔAKC + P_ΔADC = P_ΔAKL + P_ΔKLC > P_ΔAKL c.n.w.

Lolek: Dlaczego ΔADL = ΔADC ?

Blee: Masz trójkąt ADC i środkową AL ... ów środkowa dzieli pole trójkąt ADC na połowę i P_ADL = P_ADC <−−− patrz odpowiednie tw. o środkowej