Diaxowy index AGH
Licealista: Powiedzcie mi szczerze czy olimpiada o diamentowy indeks agh jest trudna. Jestem w pierwszej
klasie i marzy mi się go zdobyć. Czy te zadania w znaczacym stopniu różnią się odo matury

11 maj 01:37
Basia: AGH publikuje zadania przygotowawcze i te faktyczne z lat ubiegłych.
Poszukaj.
11 maj 01:55
Benny: Te zadania nie są trudne, jeśli nie masz w planach studia na AGH to ten konkurs możesz sobie
dopisać jako swoje własne osiągnięcie.
11 maj 02:03
11 maj 17:12
daras: nie jest trudna, kup sobe zbiór zadań z AGH i zdasz
13 maj 16:09
Basia: Z roku na rok coraz łatwiejsza.

Porównajcie edycję 2010/2011 z aktualną

13 maj 16:31
Licealista:
W 4 zadaniu za 10 pkt będzie odpowiedź
Punkt C(1,4) v C(1,0)

13 maj 21:15
Basia: z którego zestawu?
13 maj 21:26
Licealista: Z tego co przysłała pani Mila.
13 maj 21:30
Basia: Musiałam policzyć. Tak

13 maj 21:50
Mila:
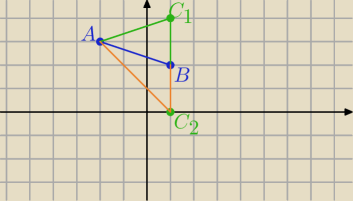
Punkty A=(−2,3) i B=(1,2) są wierzchołkami trójkąta T.
C
1=(1,4) lub C
2=(1,0)
P
Δ=3
Wsp. środka ciężkości
S
1=(0,3)
13 maj 21:58
Eta:
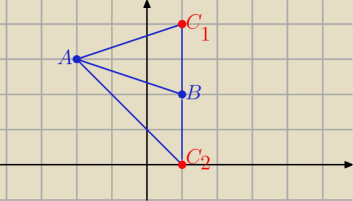
13 maj 21:58
Mila:
Licealisto, zadania staraj się przepisywać, wyjątek stanowią takie, które są trudne
do przepisania w tym edytorze (np. rysunki).
13 maj 22:00
Licealista: Macie może pomysł na zadanie 3)?
Nie wiem czy można wstawiać tutaj zadania i prosić o pomoc jak nie to wykasujcie ten post.
Znajdź liczbę p, dla której granica ciągu o wyrazie ogólnym
a
n=
3√n3+n2+9pn −
3√n3−5pn2
jest równa 2.
mianowicie spróbowałem pomnozyc to przez sprzężenie
i wyszedł wynik taki
lim(n−>+
∞)
| | n2+5pn2+9pn | |
[ |
| |
| | 3√(n3+n2+9pn)2+[3√(n3+n2+9pn)*(n3−5pn2)] +3√(n3−5pn2)2 | |
Nie mam pomysłu co zrobić dalej, a coś czuje, ze mam to zle.
13 maj 22:25
sushi:
wyciągnij w mianowniku "n2" przed nawias
w liczniku też zrób porządki: n2(....)+ n*9p
13 maj 22:31
Basia: masz dobrze;
podziel teraz licznik i mianownik przez n
2
w mianowniku "wrzuć" sobie to n
2 pod pierwiastki (czyli n
6 pod pierwiastkami)
potem "wrzuć" w nawiasy
pierwszy:
3√(n3+n2+9pn)2/n6 =
3√[(n3+n2+9pn)/n3)2 =
3√(1+(1/n)+(9pn/n2)2 → 1
drugi i trzeci też będą dążyć do 1
zostanie
tak jest łatwiej niż wyłączać spod tych pierwiastków najwyższą potegę
13 maj 22:35
Basia: Dobranoc

13 maj 22:36
Licealista : Dobranoc przemyśle to przez noc.
13 maj 23:08
Mila:
Możesz wstawiać zadania, po to forum jest. Nie można z aktualnych konkursów.
13 maj 23:12

 Porównajcie edycję 2010/2011 z aktualną
Porównajcie edycję 2010/2011 z aktualną 


 Punkty A=(−2,3) i B=(1,2) są wierzchołkami trójkąta T.
C1=(1,4) lub C2=(1,0)
PΔ=3
Wsp. środka ciężkości
S1=(0,3)
Punkty A=(−2,3) i B=(1,2) są wierzchołkami trójkąta T.
C1=(1,4) lub C2=(1,0)
PΔ=3
Wsp. środka ciężkości
S1=(0,3)

