geometria matlamp: Dany jest trójkąt o bokach długości 3, 4, 5. Tworzymy okręgi O1, O2, O3, O4, w ten sposób, że O1 jest okręgiem wpisanym w trójkąt, każdy okrąg On+1 jest styczny zewnętrznie do On i styczny do boków o długościach 4 i 5 (dla n = 1, 2, 3). Znaleźć sumę pól kół ograniczonych tymi okręgami.

matlamp: wyniki strasznie uciążliwe są tutaj, jak ktoś może to poproszę o sprawdzenie czy

	√10 −1
r2 =
	√10+1

Basia:

	3+4−5
r1 =		=1
	2

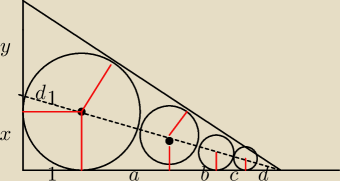
z tw.Talesa

x		1
	=
4		3

	4
x =
	3

d − długość dwusiecznej

	16		16*10
d2 = 42+(4/3)2 = 16+		=
	9		9

	4√10
d =
	3

	1		10
d12 = 12+(1/3)2 = 1+		=
	9		9

	√10
d1 =
	3

d−d₁ = √10

1		d−d1
	=
r2		1+r2

1+r₂ = √10r₂ 1 = (√10−1)r₂

	1		√10+1
r2 =		=
	√10−1		9

1		d−d1
	=
r3		d−d1−r1−2r2−r3

i tak dalej; paskudne rachunki; szukajmy prostszego sposobu

matlamp:

	1		d −d1		1		d−d1
stosunek		=		nie powinnien wyglądać tak:		=		?
	r2		1+ r2		r2		d−d1−r2

Basia: ani tak, ani tak powinien wyglądać chyba tak chyba, bo mi się w oczach mieni

1		d−d1
	=
r2		d−d1−r1−r2