Równanie ogólne prostej i prostopadły wektor Błażej: Witam, mam pytanie do równania ogólnego prostej. Otóż czy można normalnie korzystać z tego, że jeśli mamy prostą o równaniu Ax+By+C=0 to jest ona prostopadła do wektora u = [A,B]? Chodzi mi o rozwiązywanie zadań, bo już mi się parę razy zdarzyło, że dzięki tej zależności zadanie za 5 punktów robiłem w 3−4 linijkach... Chodzi mi tutaj dokładnie o to, czy egzaminatorzy na maturze mogą się do tego przyczepić.

Adamm: Raczej nie powinni się czepiać o znane twierdzenia

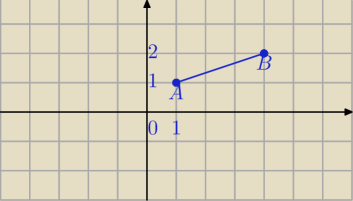
Mila: Absolutnie, nie. Chodzi tylko o poprawne zapisanie równania prostej. 1) Napisz równanie prostopadłej do AB i przechodzącej przez punkt A. 2) Napisz równanie prostej AB.

Błażej: Bo chodzi mi dokładnie tutaj o zadanie z czerwcowej matury z 2016 roku, gdzie mamy obliczyć współrzędne wierzchołka C trójkąta równoramiennego ABC, gdzie A(−7,−2) i B(4,−7) należą do podstawy, a wysokość wychodząca z punktu A zawiera się w prostej l: 2x+19y+52=0. I tutaj pojawia się pytanie. Czy mając równanie prostej (a jest ona prostopadła do wektora BC) mogę użyć tej zależności i napisać, że: BC = [x−4,y+7] i potem przyrównać poszczególne współrzędne tego wektora do współczynnika A i B prostej? Jestem ciekaw, bo jest to zadania za 5 punktów a w internecie nigdzie nie znalazłem, aby ktoś tak te zadanie rozwiązał, a jest to dość szybkie.

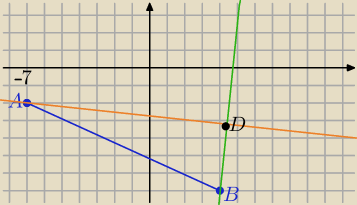
Mila: A(−7,−2) i B(4,−7) 1) l: 2x+19y+52=0 BC⊥l BC: 19x−2y+C=0 i B∊prostej BC 19*4−2*(−7)+C=0 90+C=0 C=−90 BC: 19x−2y−90=0 równanie prostej , w której zawiera sie ramię BC 2) Symetralna AB (x+7)²+(y+2)²=(x−4)²+(y+7)²⇔ s: 22x−10y−12=0 3) Punkt przecięcia prostej BC i s 22x−10y−12=0 19x−2y−90=0 ========== C=(6,12)

Mila: 1) Dla dowolnego D∊R prosta: Bx−Ay+D=0 jest prostopadła do prostej Ax+By+C=0 a także: Dla dowolnego D∊R prosta: −Bx+Ay+D=0 jest prostopadła do prostej Ax+By+C=0 Iloczyn skalarny wektorów: [B,−A], [A,B] B*A+(−A)*B=0 i (−B)*A+A*B=0 2) Przykład : k: 2x+5y+4=0 m: 5x−2y+D=0 prosta m⊥k dla dowolnego D∊R np: 5x−2y+1=0, D=1 5x−2y−6=0, D=−6 −5x+2y−6=0