Relacje kleszcz: 1. Zbadaj, które z sześciu znanych własności posiadają następujące relacje. Określ, która z relacji jest relacją a która − relacją równoważności. Wypisz wszystkie klasy abstrakcji. Mam do wykorzystania 6 relacji zwrotna, przeciwzwrotna, symetryczna, antysymetryczna, przeciwsymetryczna, przechodnia. a) R ⊂ X x X, gdzie X={a,b,c,d} i R={(a,a),(a,b),(a,c),(a,d)} Według mnie ta relacja jest tylko przeciwsymetryczna(ale mogę się mylić). Jest to relacja zwykła dla odróżnienia od relacji równoważności. Klasy abstrakcji to już nie wiem o co chodzi. b) R ⊂ X x X gdzie X={a,b,c,d} i R={(a,a),(b,b),(c,c),(d,d),(a,b),(b,a)} Według mnie ta relacja jest tylko symetryczna(ale nie jestem pewien). Relacja Zwykła c) R ⊂ X x X gdzie X={a,b,c,d,e} i R={(a,a),(b,b),(c,c),(d,d)} Według mnie to relacja antysymetryczna i relacja zwrotna(nie widzę jednak e, więc zwrotna może nie być). Relacja zwykła d) R ⊂ X x X gdzie X={a,b,c,d,e} i R={(a,b),(a,c),(b,c),(e,d),(b,a),(c,a),(c,b),(d,e)} Relacja symetryczna, relacja przeciwzwrotna i relacja przechodnia. Relacja zwykła. e) R ⊂ X x X gdzie X={a,b,c,d} i R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,c),(c,d),(d,d)} Relacja symetryczna. Relacja zwykła. f) R ⊂ X x X gdzie X={a,b,c,d} i R={(a,a),(a,b),(a,c)(d,d),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c),(d,c),(c,d)} Relacja symetryczna i Relacja Przechodnia. Relacja zwykła. Poproszę o pomoc w tym zadaniu i przede wszystkim sprawdzenie.

kleszcz: ?

Adamm: już sprawdzam

Adamm: a) antysymetryczna, przechodnia, nie jest przeciwsymetryczna klasy abstrakcji sprawdzamy dla relacji równoważności relacja zwykła − tego nie znam, chyba nie ma takiego pojęcia b) zwrotna, symetryczna c) symetryczna, antysymetryczna, przechodnia d) przeciwzwrotna, symetryczna e) zwrotna, symetryczna, przechodnia f) symetryczna

Adamm: e) jedyna relacja równoważności klasy abstrakcji [a]_R={x: (a, x)∊R}={a, b} [c]_R={x: (c, x)∊R}={c, d}

kleszcz: Ale zaraz zwrotna nie jest dla kazdego w b)?

kleszcz: W a) tez nie pasuje przechodnia...

kleszcz: Wracając do sprawy przykład a) mocno studiowałem temat i wychodzi mi rzeczywiście przechodnia oraz przeciwsymetryczna wytłumaczysz dlaczego uważasz że jest antysymetryczna i nie jest przeciwsymetryczna(?)

kleszcz: ehh ciężki ten semestr...

Adamm: przeciwsymetryczna znaczy tyle, że jeśli masz x w relacji z y, to już nie może być y w relacji z x tutaj mamy a w relacji w a gdyby relacja była przeciwsymetryczna, to a musiałoby być i nie być w relacji z a jednocześnie

kleszcz: Ale w sensie a w relacji z a jest antysymetryczne ponieważ "po zamianie miejsc" mamy to samo dokładnie i w dodatku to jest równe?

Adamm: antysymetria jest wtedy, kiedy jeśli x jest w relacji z y, i x i y są różne od siebie, to już nie może być y w relacji z x

Adamm: "a w relacji z a jest antysymetryczne" − nie ma sensu to zdanie

Adamm: relacja może być symetryczna matematyka to nie jest machanie rękami i magia

kleszcz: No ale dlaczego a) jest antysymetryczne?

Adamm: bierzemy jakiś (x, y)∊R teraz tak 1. x=y wtedy wszystko jest w porządku, możemy iść dalej 2. x≠y pytasz się, czy (y, x)∊R ? jeśli odpowiedź brzmi tak, to relacja nie jest antysymetryczna jeśli brzmi nie, to w porządku wyobraź sobie że wszystkie te elementy sprawdziłeś, i nigdy w podpunkcie drugim nie otrzymałeś (polszczyzna, taka logiczna), że relacja nie jest antysymetryczna to znaczy że jest antysymetryczna

Adamm: prościej nie potrafię

kleszcz: Czyli to chodzi że jest antysymetryczna, ponieważ ten warunek spełnia (a,a) > a=a tak dokładnie tak?

kleszcz: a jeden wystarczy bo to implikacja

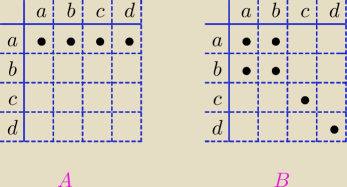
iteRacj@: ta druga zilustrowana relacja to ta opisana w punkcie B widać, że jest zwrotna (wszystkie punkty na przekątnej należą do "wykresu"), symetryczna ("wykres" jest symetryczny względem przekątnej) pierwsza zilustrowana relacja, opisana w A nie jest ani zwrotna, ani przeciwzwrotna (ani nie jest tak, że wszystkie punkty na przekątnej należą do "wykresu", ani nie jest tak, że żaden punkt na przekątnej nie należy) antysymetryczność oznacza, że z każdej pary różnych punktów symetrycznych względem przekątnej do "wykresu" należy należy tylko co najwyżej jeden przeciwsymetryczność oznacza, to co antysymetryczność ale wykluczone są punkty z przekątnej

Adamm: NIE dla każdego x i y ma spełniać

kleszcz: Nie no dla każdego to nie będzie bo to jest implikacja więc wystarczy para dla każdego to jest zwrotność i przeciwzwrotność tylko

kleszcz: dlatego mówię z tego co wiem wystarczy znaleźć parę żeby stwierdzić że coś jest antysymetryczne

kleszcz: Przynajmniej tak to tłumaczy Krystian K. u którego oczywiście zakupiłem legalnie abonament do tego tematu xD

Pytający: Tu masz definicję (słowne objaśnienie również): https://pl.wikipedia.org/wiki/Relacja_antysymetryczna Jak Adamm wspomniał, to nie jest magia. Nie rozumiesz albo kwantyfikatorów, albo kiedy implikacja jest prawdziwa, albo jeszcze czegoś innego. Zamiast negować co Ci tu napisano, postaraj się przeczytać to ponownie, ze zrozumieniem (nawet zobrazowane masz, tak się Iteracj@ postarała).

kleszcz: OK w każdym razie podpunkt f) ZWROTNA, SYMETRYCZNA, PRZECHODNIA > Równoważności tak mi wychodzi z tych praw.

kleszcz: d) PRZECIWZWROTNA, SYMETRYCZNA, PRZECHODNIA

Pytający: d) przeciwzwrotna, symetryczna Nie jest przechodnia, bo (a,b)∊R ⋀ (b,a)∊R ⋀ (a,a)∉R. f) zwrotna, symetryczna Nie jest przechodnia, bo (a,c)∊R ⋀ (c,d)∊R ⋀ (a,d)∉R.

Adamm: faktycznie, f jest zwrotna (d, d) mi umknęło

kleszcz: Na czym polega wyznaczenie klas abstrakcji, niestety słabo ten temat wyjaśniony w kursie i jaka jest definicja pojęcie "klasa abstrakcji" o co tutaj chodzi, dlaczego w tym przykładzie akurat taka klasa abstrakcji?

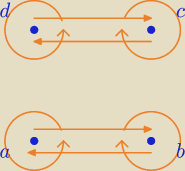
iteRacj@: e) R ⊂ X x X gdzie X={a,b,c,d} i R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,c),(c,d),(d,d)} ładnie widać na grafie tej relacji, które elementy należą do tej samej klasy abstrakcji w sieci jest dużo materiałów dotyczących klas abstrakcji