trójkat
Moc: Na przeciwprostokątnej AB trójkąta prostokątnego ABC wybrano takie punkty D i E, że AD=AC, i
BE=BC. Wykaż, że długość odcinka DE jest równa długości średnicy okręgu wpisanego w trójkąt
ABC
8 maj 15:23
Mila:
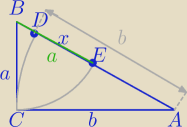
|AB|=b−x+a z treści zadania
|AB|=
√a2+b2
1) W Δ prostokątnym suma przyprostokątnych jest równa sumie średnic
okręgu wpisanego i opisanego na tym Δ⇔
a+b=2r+2R⇔
r− promień okręgu wpisanego w Δ
a+b=2r+
√a2+b2 i b−x+a=
√a2+b2⇔
2r=a+b−
√a2+b2
a+b−x=
√a2+b2
============== +
a+b−x+2r=a+b
x=2r
cnw
=======
8 maj 18:20
Mila:
|DE|=x
8 maj 18:21
 |AB|=b−x+a z treści zadania
|AB|=√a2+b2
1) W Δ prostokątnym suma przyprostokątnych jest równa sumie średnic
okręgu wpisanego i opisanego na tym Δ⇔
a+b=2r+2R⇔
r− promień okręgu wpisanego w Δ
a+b=2r+√a2+b2 i b−x+a=√a2+b2⇔
2r=a+b−√a2+b2
a+b−x=√a2+b2
============== +
a+b−x+2r=a+b
x=2r
cnw
=======
|AB|=b−x+a z treści zadania
|AB|=√a2+b2
1) W Δ prostokątnym suma przyprostokątnych jest równa sumie średnic
okręgu wpisanego i opisanego na tym Δ⇔
a+b=2r+2R⇔
r− promień okręgu wpisanego w Δ
a+b=2r+√a2+b2 i b−x+a=√a2+b2⇔
2r=a+b−√a2+b2
a+b−x=√a2+b2
============== +
a+b−x+2r=a+b
x=2r
cnw
=======