plani
oloo: W trapezie równoramiennym ABCD, w którym AB jest równoległe do CD oraz AB = 2a i CD = a,
przekątna AC zawiera się w dwusiecznej kąta DAB. Oblicz długość promienia okręgu wpisanego w
trójkąt ABC
Skąd wiadomo, że ramiona tego trapezu również równe są a? Tak pisali internecie, ale tego nie
widze.
7 maj 23:00
iteRacj@:
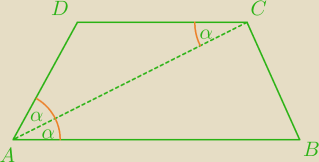
słusznie piszą w internecie
CD||AB
|<CAB|=|<ACD| kąty naprzemianległe
|<CAD|=|<ACD|=α
ΔADC równormienny ⇒ |AD|=|DC|=a
7 maj 23:37
Eta:
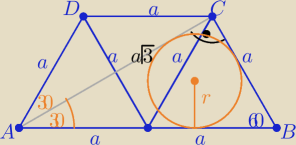
Taki trapez składa się z trzech trójkątów równobocznych o boku "a"
dł. promienia r okręgu wpisanego w trójkąt prostokątny ABC
| | a+a√3−2a | | a(√3−1) | |
r= |
| = |
| |
| | 2 | | 2 | |
8 maj 01:15
 słusznie piszą w internecie
CD||AB
|<CAB|=|<ACD| kąty naprzemianległe
|<CAD|=|<ACD|=α
ΔADC równormienny ⇒ |AD|=|DC|=a
słusznie piszą w internecie
CD||AB
|<CAB|=|<ACD| kąty naprzemianległe
|<CAD|=|<ACD|=α
ΔADC równormienny ⇒ |AD|=|DC|=a
 Taki trapez składa się z trzech trójkątów równobocznych o boku "a"
dł. promienia r okręgu wpisanego w trójkąt prostokątny ABC
Taki trapez składa się z trzech trójkątów równobocznych o boku "a"
dł. promienia r okręgu wpisanego w trójkąt prostokątny ABC