zad Krzysiekmatura: wow, właśnie zrozumiałem skąd sie bierze wzór na równanie stycznej do wykresu funkcji: y=f′(x₀)(x−x₀)+f(x₀)

PW: Powiedziałbym nawet, że dla funkcji różniczkowalnej w x₀ jest to definicja stycznej do wykresu funkcji w punkcie (x₀, f(x₀).

Krzysiekmatura: Natknąłem się na takie zadanie: http://www.free-test-online.com/world/csat1.html Nie rozumiem czemu rozwiązanie równania po obustronnym zróżniczkowaniu daje nam x styczności

Krzysiekmatura: Ktoś wie?

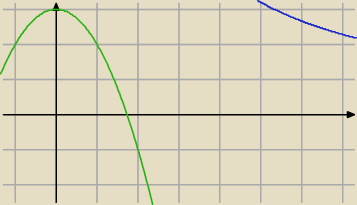
PW: Niebieska i zielona są różniczkowalne. Jeżeli stykają się tylko w jednym punkcie, to mają w tym punkcie wspólną styczną, a więc jednakowe pochodne f'(x)=g'(x)

	16
−		=−2x
	x2

x=2. x₀=2 jest pierwszą współrzędną punktu styczności wykresów. W takim razie punkt styczności wyznacza a: f(0)=g(0)

	16
		=−22+a
	2

12 = a. Jak widać na ilustracji wybrano za małe a. Wykonaj rysunek dla a=12.

PW: Korekta. W czwartym wierszu od dołu f(x₀)=g(x₀)

Krzysiekmatura: Dzięki, stwierdzenie "mają w tym punkcie wspólną styczną, a więc jednakowe pochodne" wyjaśniło wszystko