Dla jakiej wartości parametru m rozwiązaniem równania jest para liczb... signumy: Dla jakiej wartości parametru m rozwiązaniem równania |x−1| = m+2 jest para liczb o przeciwnych znakach? Mam takie oto gotowe rozwiązanie: |x−1|=m+2 ⇒ x−1 = m+2 dla x−1≥ 0 −x +1 =m+2 dla x−1<0 I teraz nie rozumiem tego dalej: x=m+3 dla x≥1 x= −m−1 dla x<1 m+3≥1 ⇒ m≥−2 −m−1<0 m>−1 Te dwie ostatnie linijki kompletnie nie mam pomysłu dlaczego tak jest

Tadeusz: to Ty prostych przekształceń nie ogarniasz?

signumy: Tadeusz ten komentarz raczej mi nie pomaga

signumy: Nie ogarniam, że skoro mieliśmy x=−m−1 dla x<1 i nagle mamy −m−1<0

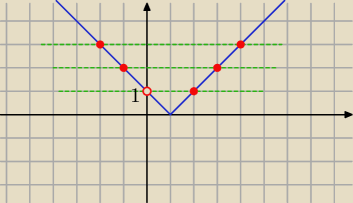
Eta: wykres y=|x−1| i tniesz prostymi y= m+2 Rozwiązaniem jest para liczb o przeciwnych znakach dla m+2>1 ⇒ m>−1 ===== i po "ptokach"

signumy: O, jasne i przejrzyste rozwiązanie. Dziękuję Eta

piotr: rozwiązanie x=m+3 dla x≥1 będzie dodatnie a rozwiązanie x= −m−1 dla x<1 będzie wtedy ujemne ⇒ (m+3>0 ∧ m+3≥1) ∧ (−m−1<0 ∧ −m−1<1) ⇒ m>−1

PW: Równanie ma postać |x−1|=m+2 − lewa strona jest nieujemna, zatem musi być nieujemna i prawa: m+2≥0 m≥−2 Wniosek: Dla m<−2 nie ma rozwiązań. Dla m=−2 mamy równanie |x−1|=0 o jednym rozwiązaniu.. Dla m>−2 równanie |x−1|=m+2 ma dwa rozwiązania: x−1=m+2 lub x−1=−(m+2) x=m+3 lub x=−m−1, m>−2 Rozwiązania te są przeciwnych znaków, gdy ich iloczyn jest ujemny: (m+3)(−m−1)<0, m>−2 (m+3)(m+1)>0, m>−2. Narysować parabolę, wynik m>−1

Eta:

signumy: Dzięki piotr

signumy: Dziękuję PW